Η λογική της αιτιώδους-φυλλικής σηματοδότησης
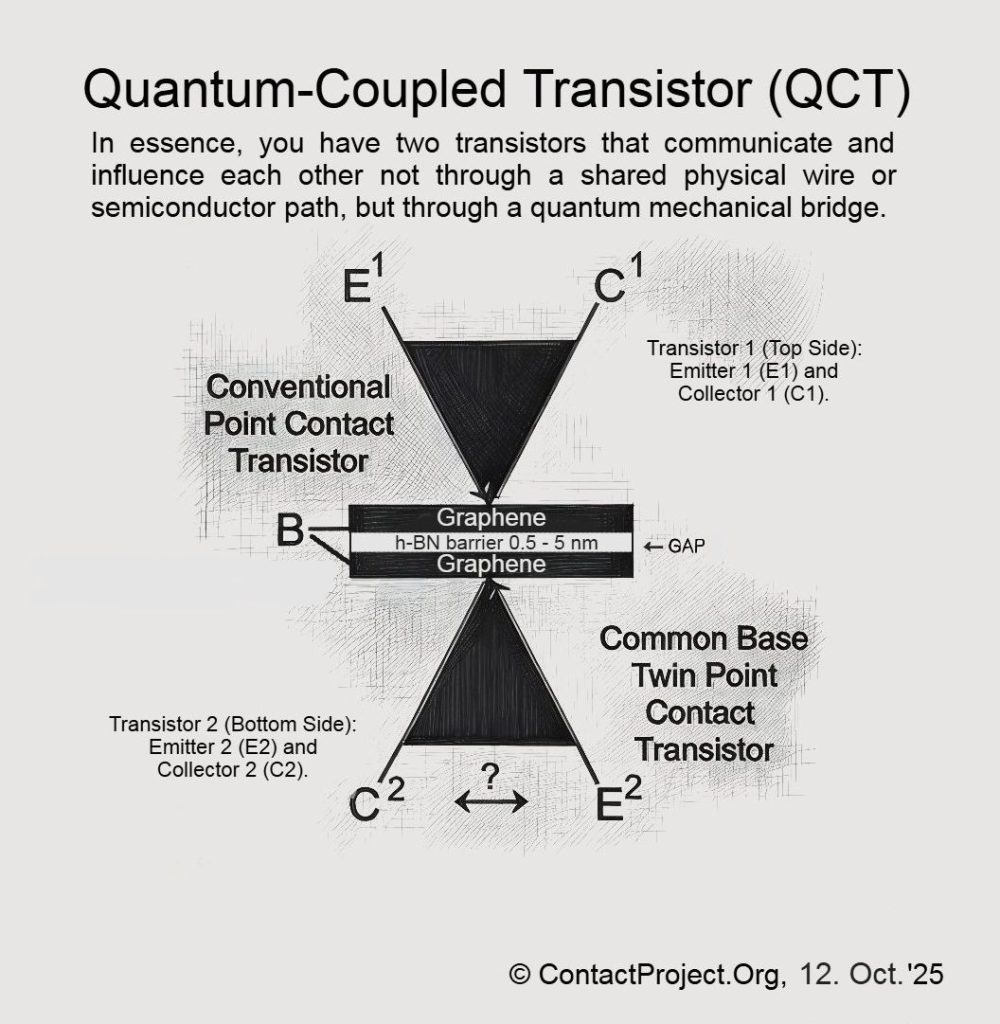
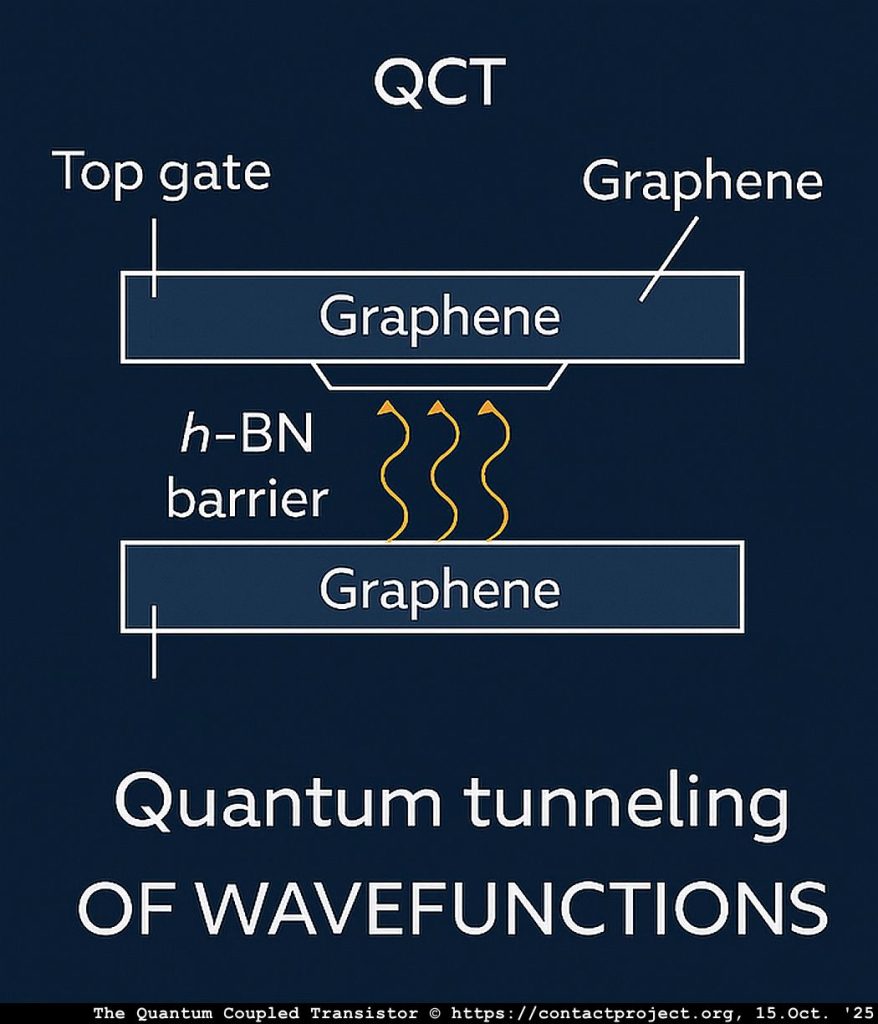
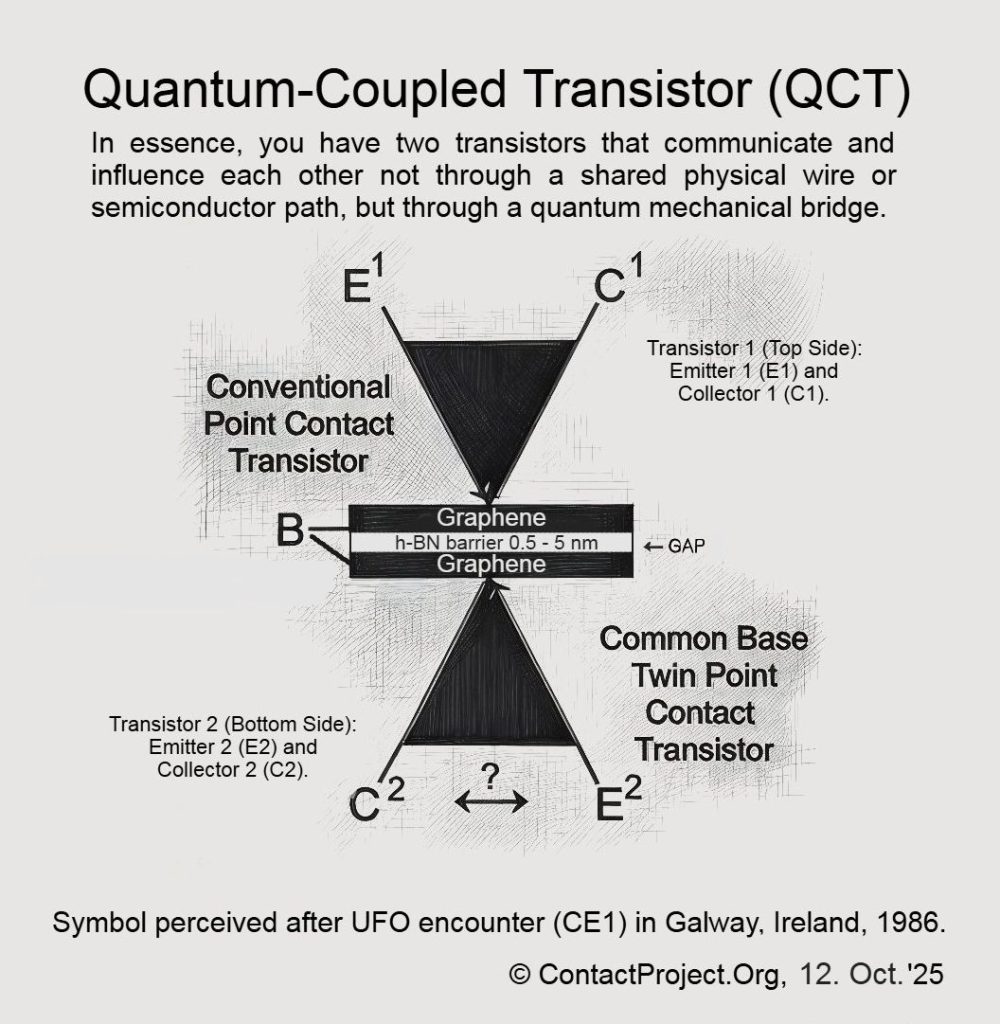
Η θεωρία του Αιτιώδης-Φυλιασμένη Σηματοδοσία (CFS) προτείνει ότι ο χρόνος περιέχει κρυφά στρώματα που επιτρέπουν περιορισμένη συνοχή μεταξύ κβαντικών συστημάτων, ταχύτερη από το φως. Οι ερευνητές μπορεί σύντομα να χρησιμοποιήσουν το Κβαντικό Συζευγμένο Τρανζίστορ (QCT) – μια νανοσυσκευή διπλού γραφενίου – για να δοκιμάσει άμεσα αυτά τα φαινόμενα και να προσδιορίσει εάν μπορούν να συμβούν χωρίς να παραβιαστούν οι γνωστοί νόμοι της φυσικής.
Στην ουσία του, το CFS θέτει ένα προκλητικό ερώτημα: Τι θα γινόταν αν ορισμένα είδη κυμάτων, όπως τα εξαφανιζόμενα ή τα κοντινά πεδία, μπορούσαν να μοιράζονται πληροφορίες φάσης ταχύτερα από το φως, διατηρώντας παράλληλα την αιτιότητα;
Αν ναι, ο χωροχρόνος μπορεί να μην είναι απόλυτα ομοιόμορφος. Θα μπορούσε να περιέχει μια λεπτή εσωτερική δομή – μια «στρωματοποίηση» χρόνου, όπου οι πληροφορίες κινούνται ελαφρώς προς τα εμπρός μέσα σε κάθε στρώση, ενώ παραμένουν συνεπείς σε όλο το σύνολο.

Από αυτή την άποψη, το σύμπαν ξεδιπλώνεται σαν τις σελίδες ενός τεράστιου κοσμικού βιβλίου: κάθε σελίδα γυρίζει με τέλεια σειρά, ακόμα κι αν κάποιες γυρίζουν λίγο πιο γρήγορα από άλλες. Το CFS προσφέρει μια εκλεπτυσμένη θεώρηση της σχετικότητας – μια θεώρηση που επιτρέπει δομημένη υπερφωτεινή συνοχή, διατηρώντας παράλληλα την ιστορία της αιτίας και του αποτελέσματος άθικτη.
Μέρος II. Αιτιώδης-Φολιατοειδής Σηματοδοσία (CFS)
- Βασικά Αξιώματα
- Κινηματική και Δυναμική
- Κβαντικοί Κανόνες και Διατήρηση
- Πειραματικές προβλέψεις
- Πρωτόκολλα δοκιμής
- Ο ρόλος του QCT
1. Βασικά Αξιώματα
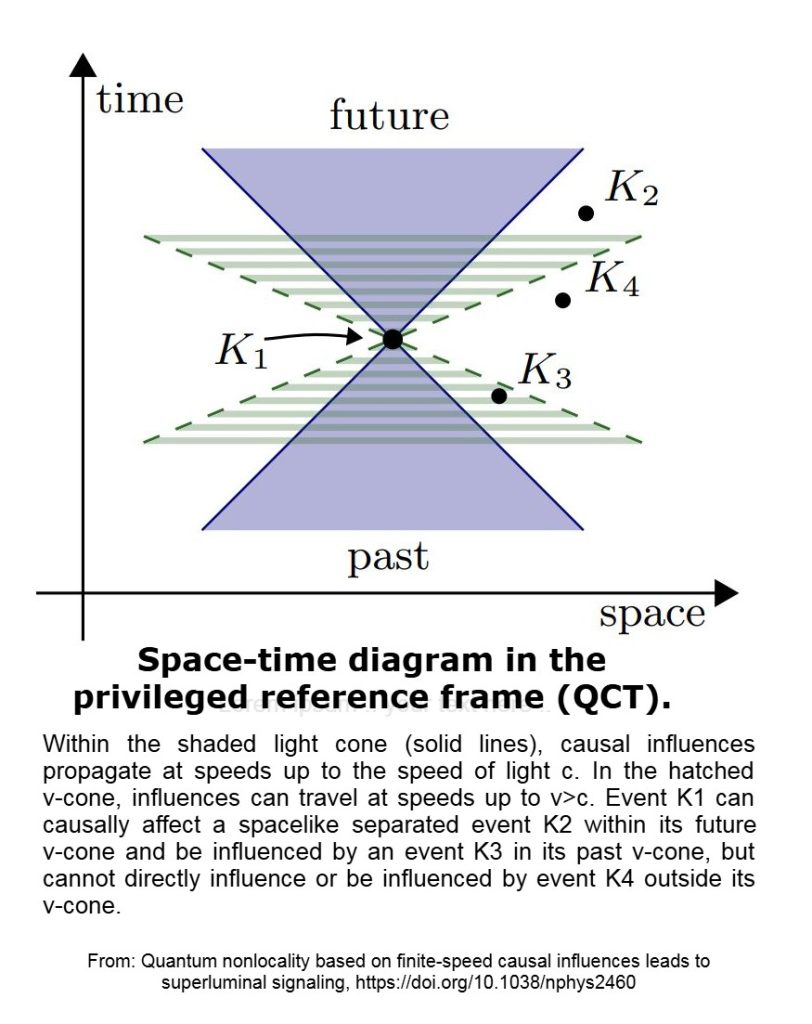
- Παγκόσμια Χρονική Φυλίωση: Ο χωροχρόνος διαθέτει μια προτιμώμενη καθολική τεμαχισμό (κοσμικός χρόνος, που ορίζεται από χρονόμορφο διάνυσμα uᵃΌλα τα σήματα – φωτεινά και υπερφωτεινά – ταξινομούνται με βάση αυτή την φυλλοποίηση.
- Διευρυμένος κώνος σήματος: Πέρα από τον κώνο φωτός, υπάρχει ένας ευρύτερος «κώνος σήματος» για συγκεκριμένα μέσα ή πεδία (χ).
- Προστασία Χρονολογίου: Οι κλειστοί βρόχοι σήματος απαγορεύονται δυναμικά από περιορισμούς επιλυτότητας.
- Επιχειρησιακή Τοποθεσία: Τα τυπικά πειράματα παραμένουν αμετάβλητα ως προς τον Lorentz. Αποκλίσεις εμφανίζονται μόνο εντός των ενεργοποιημένων μέσων.
2. Κινηματική και Δυναμική
- Προτιμώμενο Πλαίσιο: Ευθυγραμμισμένο περίπου με το πλαίσιο στήριξης CMB.
- Πεδίο σήματος (χ): Συνδέεται ασθενώς με φορείς ηλεκτρομαγνητικών κυμάτων, διευρύνοντας τον αιτιώδη κώνο.
- Υπερβολικά χαρακτηριστικά: ΜΔΕ σε ενεργοποιημένα μέσα παρουσιάζουν διάδοση εκτός του κώνου g-φωτός.
- Περιορισμός χωρίς βρόχο: Οι ολοκληρωτικές συνθήκες αποτρέπουν τους χρονικά μειούμενους αιτιακούς βρόχους.
3. Κβαντικοί Κανόνες και Διατήρηση
Κατασκευάσαμε μια μικροσκοπική περιοχή (το κενό QCT) όπου τα κβαντικά κοντινά πεδία μπορούν να διαμορφωθούν απαλά έτσι ώστε ένα μόλις ανιχνεύσιμο, ταχύτερο από το φως πρότυπο εμφανίζεται σε κατά τα άλλα τυχαία δεδομένα – αρκετά μικρό για να διατηρεί τη φυσική ασφαλή, αρκετά καθαρό για να το δοκιμάσει κανείς στο εργαστήριο.

Αν η παραπάνω συνοπτική δήλωση σας φαίνεται λογική, τότε μπορείτε να επεκτείνετε την κόκκινη γραμμή Κβαντικοί Κανόνες παρακάτω κάνοντας κλικ στα μαύρα ▶ τρίγωνα, για μια ΠΙΟ λεπτομερή συζήτηση.
Για τους γενικούς αναγνώστες, κάθε ενότητα περιλαμβάνει μια σύντομη εξήγηση (χωρίς μαθηματικά) ακολουθούμενη από μια αναλογία. Αν και οι περισσότεροι άνθρωποι δεν θα έχουν ακούσει ποτέ για θεώρημα μη επικοινωνίας (απαγορεύοντας την επικοινωνία με ταχύτητες ταχύτερες από το φως... μέσω εμπλοκής), τοποθετείται σε περίοπτη θέση εδώ λόγω της θεμελιώδους σημασίας του και επειδή ελέγχεται χαλάρωση αυτού του κανόνα εξερευνάται εδώ.
[κάντε κλικ για άνοιγμα] Θεώρημα Χαλαρής Μη Επικοινωνίας: Σε ενεργοποιημένα μέσα, οι μη γραμμικές/μετα-επιλεγμένες δυναμικές επιτρέπουν ελάχιστη κλασική χωρητικότητα > 0.
Αξίωση (λειτουργική):
Σε μία ενεργοποιημένο μέσο (π.χ., ένα κενό QCT που λειτουργεί ως χ-ενεργοποιημένο κοντινό πεδίο), ένα ασθενής, εντοπισμένη μη γραμμικότητα or ρητή επιλογή μετά την ολοκλήρωση της διαδικασίας μπορεί να παράγει ένα μικρή αλλά πεπερασμένη κλασική χωρητικότητα C>0 μεταξύ χωρικά διαχωρισμένων μερών χωρίς να παραβιάζεται η παγκόσμια μοναδιαρχία ή ο κανόνας του Born.
Ρύθμιση
Ας ρAB να είναι μια διμερής κατάσταση που μοιράζονται η Αλίκη και ο Μπομπ. Σε τυπική QM με τοπικό Χάρτες CPTP και Όχι. μετά την επιλογή, η ανηγμένη κατάσταση του Μπομπ είναι ανεξάρτητη από την επιλογή της Αλίκης:
ρB′ = TrA [(ΦA⊗IB)(ρAB)] = ρB, (χωρίς σηματοδότηση)
Σε μία ενεργοποιημένη περιοχή QCT, μοντέλο ελεγχόμενης λειτουργίας της Alice ως ασθενώς μη γραμμικό διαταραχή ενός Χάρτης CPTP:
ΦA(V)(⋅)=ΛA(⋅)+ε\mathcal{N}_A^{(V)}[⋅], 0<ε≪1,[/latex] όπου [λάτεξ]V είναι ο έλεγχος της Alice (π.χ., μεροληψία μεταξύ των στρώσεων), ΛΑ είναι το CPTP και \mathcal{N}_A^{(V)} είναι μια φραγμένη μη γραμμική συνάρτηση που ενεργεί μόνο εντός του χ-ενεργοποιημένο μέσο.Η κατάσταση του Μπομπ γίνεται
ρB′(V)=TrA[(ΦA(V)⊗IB)ρAB]=ρB(0)+εΔρB(V),μαζί σου,
ΔρB(V)=TrA [(NA(V)⊗IB)ρAB].\Δέλτα\rho_B(V)=\mathrm{Tr}_A\!\Big[\big(\mathcal{N}_A^{(V)}\φορές \mathbb{I}_B\big)\rho_{AB}\Big].ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].
If \Δέλτα\rho_B(V_0)\neq \Δέλτα\rho_B(V_1), τότε τα στατιστικά στοιχεία του αποτελέσματος του Μπομπ εξαρτώνται (ελαφρώς) από την επιλογή της Αλίκης V, επιτρέποντας την κλασική επικοινωνία κατά παραγγελία \varepsilon.
Για μια οπτική γωνία θέασης (POM) \{Μου\} στον Μπομπ, οι πιθανότητες ανίχνευσης είναι
P(y∣V)=Tr[MyρB′(V)]=P0(y)+εΔP(y∣V),ΔP(y∣V):=Tr[MyΔρB(V)].Χωρητικότητα με ασθενή σηματοδότηση
Αφήστε την Αλίκη να στείλει ένα δυαδικό σύμβολο X\in\{0,1\} Επιλέγοντας V\in\{V_0,V_1\}.. Ο Μπομπ μετρά Y\in\{0,1\}. Καθορίζω
\delta := P(Y=1\mid V_1)-P(Y=1\mid V_0)=\varepsilon\,\Delta P + O(\varepsilon^2),με πιθανότητα σφάλματος βάσης p:=P(Y=1∣V0).
Για ένα κανάλι δυαδικής εισόδου, δυαδικής εξόδου στο όριο μικρού σήματος ∣\δέλτα|\ll 1, Χωρητικότητα Shannon παραδέχεται την τετραγωνική προσέγγιση
C περίπου; \frac{\δέλτα^2}{2\ln 2}\,\frac{1}{p(1-p)} +\; O(\δέλτα^4), \qquad C>0\ \text{iff}\ \δέλτα\neq 0.
Έτσι, οποιοδήποτε μη μηδενικό \δέλτα (επομένως, κάθε μη μηδενικό \varepsilon-εξάρτηση από την παραγγελία V) αποδίδει ένα πεπερασμένος C>0.
Ο ρόλος της μετεπιλογής
Αν ο Μπομπ (ή ένα κύκλωμα σύμπτωσης με άρθρωση) μετά την επιλογή σε ένα παράθυρο αποτελεσμάτων W με πιθανότητα επιτυχίας pW, υπό όρους κράτος είναι
\rho_{B\!\mid W}(V)\;=\;\frac{\Pi_W\,\rho_B'(V)\,\Pi_W}{\mathrm{Tr}\!\big[\Pi_W\,\rho_B'(V)\big]}, \qquad \Pi_W=\Pi_W^\dagger=\Pi_W^2.Λόγω της ομαλοποίησης από \mathrm{Tr}[\Pi_W\rho_B'(V)], η χαρτογράφηση \rho'_B \mapsto \rho_B^{\mid W} is μη γραμμικό, και οι εξαρτημένες στατιστικές μπορούν να αποκτήσουν ένα V-εξάρτηση ακόμα και όταν χωρίς όρους Ισχύει η ισότητα μη σηματοδότησης. Στην πράξη, η μετα-επιλογή κλιμακώνει τον χρήσιμο ρυθμό κατά pW:
C_{\mathrm{eff}} \approx p_W, C.Συνθήκες συνέπειας
Για την αποφυγή γενικευμένων παθολογιών:
- Εντοπισμός: \mathcal{N}_A^{(V)} περιορίζεται στο χ-ενεργοποιημένη περιοχή (π.χ., το κενό QCT).
- Μικρότητα: \varepsilon είναι αρκετά μικρό για να διατηρήσει τη σταθερότητα και τα ενεργειακά όρια.
- Παγκόσμια μοναδικότητα και κανόνας Born: Η δυναμική του συνόλου παραμένει CPTP. Οι αποκλίσεις (εάν υπάρχουν) περιορίζονται στους εξαρτημένους, τοπικούς χάρτες ανιχνευτών (μετά την επιλογή) ή στον ασθενή-μη γραμμικό τομέα μέσα στο μέσο.
Συμπαγής δήλωση
\boxed{ \begin{aligned} &\Phi_A^{(V)}=\Lambda_A+\varepsilon\,\mathcal{N}_A^{(V)},\quad \varepsilon\ll 1,\\ &\rho_B'(V)=\rho_B^{(0)}+\varepsilon\,\Delta\rho_B(V),\quad \Delta\rho_B(V)=\mathrm{Tr}_A\!\big[(\mathcal{N}_A^{(V)}\!\times\!\mathbb{I})\,\rho_{AB}\big],\\ &\exists\,M:\ \delta=\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_1)\big]-\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_0)\big]\neq 0 \\ &\Rightarrow\ C \approx \dfrac{\delta^2}{2\ln 2\, p(1-p)} \;>\;0,\quad C_{\text{eff}}\approx p_W\,C\ \text{(με μετα-επιλογή)}. \end{aligned}}Ακολουθεί μια ανάλυση και επαλήθευση γεγονότων της συμπαγούς μαθηματικής πρότασης:
Η μαθηματική πρόταση είναι μια αναπαράσταση ενός αποτελέσματος στην κβαντική θεωρία πληροφοριών, που σχετίζεται με τον υπολογισμό της χωρητικότητας ενός κβαντικού καναλιού με μια μικρή διαταραχή. Συνδέει τη φυσική περιγραφή ενός κβαντικού καναλιού με την προκύπτουσα χωρητικότητα καναλιού, ενσωματώνοντας έννοιες όπως η διαταραχή κατάστασης, η διακριτότητα των καταστάσεων εξόδου και η επίδραση της μετα-επιλογής. Ας αναλύσουμε κάθε μέρος για να επαληθεύσουμε τα συστατικά του:
Διαταραχή Καναλιού και Κατάστασης
\Φ_Α(V) = \Λάμδα_Α + \έψιλον N_A(V), \έψιλον \ll 1Αυτό περιγράφει ένα κβαντικό κανάλι \Φι_Α που επενεργεί σε ένα σύστημα Α. Αποτελείται από ένα κυρίαρχο, σταθερό μέρος \Λάμδα_Α και μια μικρή αναστάτωση \έψιλον N_A(V), Όπου \έψιλο είναι μια μικρή παράμετρος και το V είναι κάποια ελεγχόμενη παράμετρος του καναλιού. Αυτός είναι ένας τυπικός τρόπος αναπαράστασης ενός ελαφρώς διαμορφωμένου ή θορυβώδους κβαντικού καναλιού. \rho_B'(V) = \rho_B(0) + \έψιλον \Δrho_B(V)Αυτό δείχνει την επίδραση του καναλιού σε ένα μέρος μιας ευρύτερης κβαντικής κατάστασης. Υποδεικνύει ότι η κατάσταση εξόδου ενός υποσυστήματος Β, \rho_B'(V), είναι μια ελαφρώς διαταραγμένη εκδοχή μιας αρχικής κατάστασης \rho_B(0)Η διαταραχή \Δλ_ρ_Β(V) είναι ανάλογο με τη μικρή παράμετρο \έψιλο. \Δέλτα\rho_B(V) = Tr_A[(N_A(V) \φορές I)\rho_{AB}]Αυτή είναι η σαφής μορφή της διαταραχής πρώτης τάξης στην κατάσταση του συστήματος Β. Προκύπτει λαμβάνοντας το μερικό ίχνος (Tr_A) πάνω από το σύστημα Α της δράσης του διαταρακτικού μέρους του καναλιού σε μια μεγαλύτερη, εμπλεκόμενη κατάσταση \rho_{AB}Αυτή είναι μια τυπική και σωστή εφαρμογή των κανόνων της κβαντομηχανικής.
Διακριτότητα των Κρατών
\υπάρχει M: \δέλτα = \epsilon Tr[M\Delta\rho_B(V_1)] - \epsilon Tr[M\Delta\rho_B(V_0)] \neq 0Αυτό είναι το κρίσιμο βήμα για τον καθορισμό μιας μη μηδενικής χωρητικότητας καναλιού. Δηλώνει ότι υπάρχει ένας τελεστής μέτρησης (ένας τελεστής Ερμιτιανός) M που μπορεί να διακρίνει μεταξύ των διαταραγμένων καταστάσεων που αντιστοιχούν σε δύο διαφορετικές ρυθμίσεις της παραμέτρου καναλιού, V_1 και V_0Η ποσότητα \δέλτα αντιπροσωπεύει τη διαφορά στην αναμενόμενη τιμή της μέτρησης M για τις δύο καταστάσεις εξόδου. Το γεγονός ότι \δέλτα \νεξίσωση 0 είναι η προϋπόθεση για να είναι οι δύο καταστάσεις πειραματικά διακριτές, τουλάχιστον κατ' αρχήν.
Χωρητικότητα καναλιού
C \περίπου \frac{\δέλτα^2}{2\ln{2}p(1-p)} > 0Αυτό είναι ένα βασικό αποτέλεσμα, πιθανώς μια προσέγγιση για τη χωρητικότητα Holevo ή ένα σχετικό μέτρο της χωρητικότητας καναλιού στο όριο των μικρών \δέλταΗ χωρητικότητα C είναι ένα μέτρο του μέγιστου ρυθμού με τον οποίο οι πληροφορίες μπορούν να σταλούν αξιόπιστα μέσω του καναλιού. Ο όρος \δέλτα^2 αναμένεται, καθώς η χωρητικότητα συχνά κλιμακώνεται με το τετράγωνο της διακριτότητας των καταστάσεων εξόδου για μικρές διαταραχές. Ο παράγοντας του 2\ln{2} είναι το πρότυπο για τη μετατροπή από φυσικές μονάδες πληροφοριών (nats) σε bits. Ο όρος p(1-p) στον παρονομαστή υποδηλώνει ότι η χωρητικότητα αξιολογείται για ένα συγκεκριμένο σύνολο εισόδων, όπου οι δύο καταστάσεις (που αντιστοιχούν σε V_0 και V_1) χρησιμοποιούνται με πιθανότητες p και 1-p. Η χωρητικότητα μεγιστοποιείται όταν p=1/2, η οποία αποτελεί κοινή παραδοχή.
Αποτελεσματική Χωρητικότητα με Μετά την Επιλογή
C_{eff} \περίπου p_W C (με μετα-επιλογή): Αυτό το μέρος της δήλωσης περιγράφει την αποτελεσματική χωρητικότητα όταν χρησιμοποιείται η μετα-επιλογή. Η μετα-επιλογή είναι μια τεχνική όπου λαμβάνεται υπόψη μόνο ένα υποσύνολο των αποτελεσμάτων μέτρησης, το οποίο μερικές φορές μπορεί να ενισχύσει ένα ασθενές σήμα. p_W θα ήταν η πιθανότητα μιας επιτυχούς μετά την επιλογή (η «πιθανότητα μετά την επιλογή»). Η αποτελεσματική χωρητικότητα C_{eff} μειώνεται κατά αυτήν την πιθανότητα επειδή πολλές από τις αρχικές καταστάσεις απορρίπτονται. Αυτή είναι μια γνωστή αντιστάθμιση στα σχήματα μετά την επιλογή: μπορεί να λάβετε ένα πιο καθαρό σήμα, αλλά χάνετε ένα σημαντικό μέρος των δεδομένων σας, μειώνοντας έτσι τον συνολικό ρυθμό μετάδοσης πληροφοριών.
Έλεγχος στοιχείων τεχνητής νοημοσύνης: Συμπέρασμα
Οι μαθηματικές εκφράσεις είναι σύμφωνες με τις καθιερωμένες αρχές της κβαντικής θεωρίας πληροφοριών. Η λογική ρέει σωστά από τον ορισμό ενός διαταραγμένου κβαντικού καναλιού έως τη διακριτότητα των καταστάσεων εξόδου του και τέλος σε μια έκφραση για τη χωρητικότητα του καναλιού. Η συμπερίληψη της επίδρασης της μετα-επιλογής είναι επίσης τυπική. Επομένως, τα μαθηματικά στη συμπαγή πρόταση φαίνεται να είναι σωστά και αντιπροσωπεύουν μια έγκυρη συλλογιστική στο πλαίσιο της χωρητικότητας του κβαντικού καναλιού.
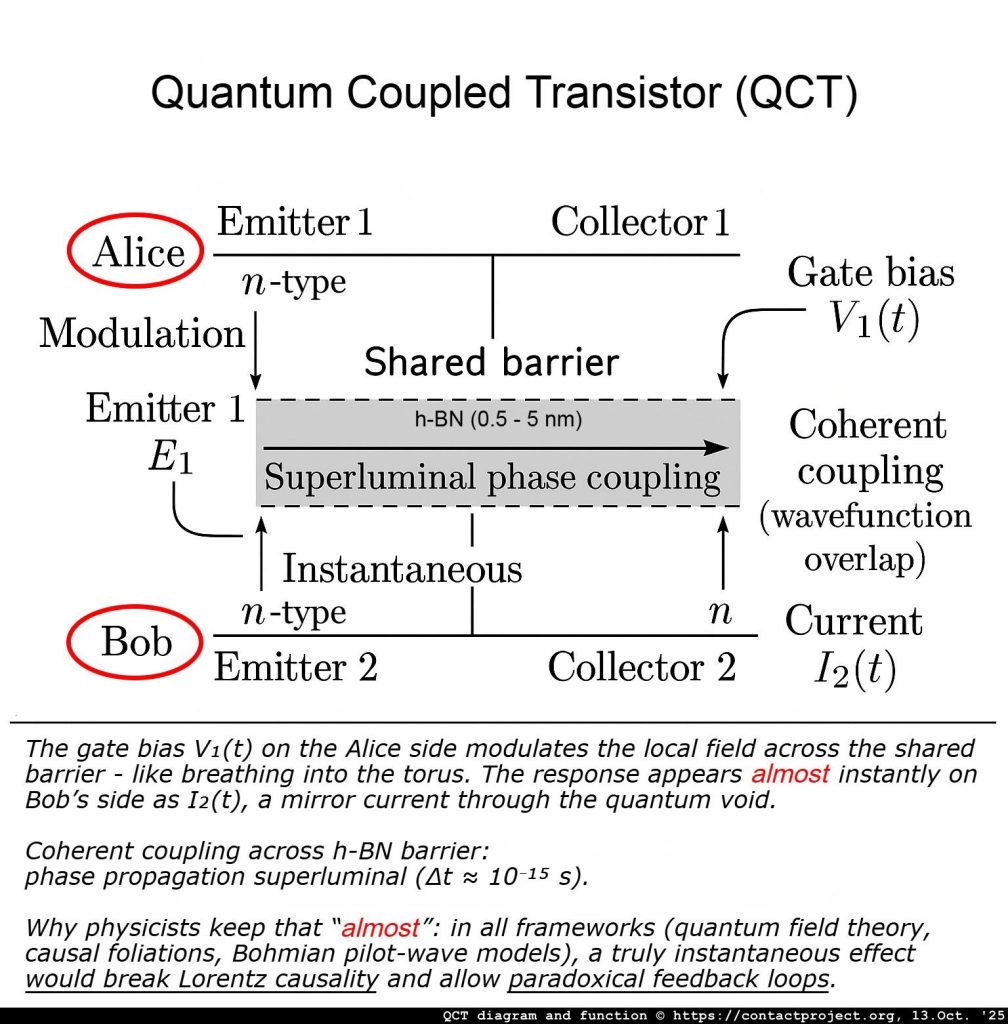
QCT: Παρουσιάζοντας την Άλις και τον Μπομπ
In τυπική κβαντική θεωρία και επιστήμη της πληροφορίας, Αλίκη και Βαρίδι είναι οι κλασικοί αναπληρωτές - οι πειραματιστές του «κάθε ατόμου» που χρησιμοποιούνται για να δείξουν πώς συμπεριφέρονται τα κβαντικά συστήματα όταν δύο μέρη μοιράζονται πληροφορίες.

Εμφανίστηκαν για πρώτη φορά στις αρχές της δεκαετίας του 1970: Η Άλις ήθελε να στείλει ένα μήνυμα στον Μπομπ, ενώ ένας κρυφοκώστας, Εύα, προσπάθησαν να την αναχαιτίσουν. Η ιδέα έγινε ευρέως διαδεδομένη και οι φυσικοί σύντομα υιοθέτησαν τα ίδια ονόματα για να περιγράψουν τα κβαντικά πειράματα - ειδικά εκείνα που περιελάμβαναν μπλέξιμο, τηλεμεταφοράκαι τα όρια της επικοινωνίας.
Στην κβαντομηχανική, η Άλις και ο Μπομπ συνήθως λειτουργούν δύο ξεχωριστά εργαστήρια. Μοιράζονται ένα ζεύγος πεπλεγμένων σωματιδίων και εκτελούν τις μετρήσεις τους ανεξάρτητα. Ωστόσο, παρόλο που τα αποτελέσματα συσχετίζονται, κανένα από τα δύο δεν μπορεί να τα χρησιμοποιήσει για να στείλει ένα μήνυμα ταχύτερα από το φως. Στην τυπική κβαντική θεωρία, οι τοπικές μετρήσεις μοιάζουν πάντα με λευκό θόρυβο - μέχρι αργότερα να συγκρίνουν τις σημειώσεις και να αναδυθεί το κρυφό μοτίβο.
Η δική μας ανατροπή (μόνο εντός του ενεργοποιημένου μέσου): σε μια πολύ συγκεκριμένη, μηχανικά σχεδιασμένη ζώνη - όπως η χάσμα h-BN του QCT - μικροσκοπικά, προσεκτικά περιορισμένα μη γραμμικά φαινόμενα ή επιλογή μετά την επιλογή «διατήρηση μόνο αυτών των γεγονότων» μπορούν να μετατρέψουν ένα μικροσκοπικό μέρος αυτού του θορύβου σε πολύ αχνό αλλά πραγματικό σήμαΕίναι ακόμα μικροσκοπικό, αλλά δεν είναι πλέον λευκός θόρυβος.
Καθημερινή αναλογία: μια καταιγίδα στατικού ηλεκτρισμού σε ένα ραδιόφωνο (τυχαία), αλλά αν διαμορφώσετε ελαφρώς την κεραία και επιλέξετε μόνο τις σωστές στιγμές, ακούγεται ένας ψίθυρος ενός σταθμού. Η καταιγίδα είναι ακόμα εκεί, αλλά τώρα ένα μοτίβο την ακολουθεί.
Ρύθμιση (ποιος κάνει τι)
Δύο κόμματα - Αλίκη και Βαρίδι - μοιράζονται μια συσχετισμένη κβαντική ρύθμιση. Κανονικά, ό,τι κάνει η Αλίκη τοπικά δεν να αλλάξει αυτό που βλέπει ο Μπομπ μόνος του. Μέσα στο κενό QCT, ο έλεγχος της Αλίκης (ένα μικροσκοπικό, υψηλής ταχύτητας μοτίβο πόλωσης) αναδιαμορφώνει ελαφρώς τους τοπικούς κανόνες μέτρησης από την πλευρά της με τρόπο που έχει σημασία μόνο μέσα αυτό το κενό. Αυτή η μικροσκοπική αναμόρφωση μπορεί να αφήσει ένα δακτυλικό αποτύπωμα σχετικά με το τι μετρά ο Μπομπ - εξακολουθεί να είναι θορυβώδες συνολικά, αλλά τώρα στατιστικά ώθησε με επιλογή της Αλίκης.
Αναλογία: Η Άλις κουνάει έναν φακό πίσω από ένα αδιαφανές τζάμι (το φράγμα σήραγγας). Ο Μπομπ δεν μπορεί να δει τον φακό, αλλά μια μόλις ορατή λάμψη στο πλάι του αλλάζει σε αρμονία με το μοτίβο κουνήματος της.

Τι πρέπει να δει ο Μπομπ (το καπνιστικό όπλο)
Αν δεν συμβαίνει τίποτα πέρα από τους τυπικούς κβαντικούς κανόνες, τα δεδομένα του Μπομπ μοιάζουν με τυχαία ρίψη νομισμάτων - κανένα μοτίβο δεν συνδέεται με τις επιλογές της Αλίκης. Αν το ενεργοποιημένο μέσο κάνει πραγματικά τη δουλειά του, έπειτα θαμμένο στα θορυβώδη δεδομένα του Μπομπ είναι ένα μικροσκοπική, επαναλήψιμη συσχέτιση με το μοτίβο της Αλίκης - ανιχνεύσιμο με διασταύρωση χρονικών σημάνσεων και, κυρίως, εμφάνιση πριν οποιοδήποτε συνηθισμένο σήμα με ταχύτητα φωτός θα μπορούσε να φτάσει (>Γ).
Αναλογία: δύο ντράμερ μακριά ο ένας από τον άλλον· αν το μικρόφωνο του Μπομπ ακούει έναν αμυδρό χτύπο ευθυγραμμισμένο με τον ρυθμό της Άλις πριν ο ήχος προλάβει να ταξιδέψει, κάτι ασυνήθιστο τους συνδέει.
«Χωρητικότητα» (πόσο μήνυμα χωράει)
Σκέφτομαι ικανότητα όπως πόσα bits ανά δευτερόλεπτο μπορείτε να περάσετε μέσα από αυτό το αμυδρό εφέ.
- Αν η συσχέτιση είναι αληθής μηδέν, η χωρητικότητα είναι μηδέν - κανένα μήνυμα.
- Αν η συσχέτιση είναι μικροσκοπικό αλλά μη μηδενικό, η χωρητικότητα είναι μικροσκοπικό αλλά μη μηδενικό - μπορείτε να στείλετε μερικοί πληροφορίες (αργά), και αυτό είναι ήδη κάτι σημαντικό από φυσικής άποψης.
Αναλογία: Η Άλις περνάει ένα μήνυμα μέσα από έναν χοντρό τοίχο. Κάθε χτύπημα μετά βίας φτάνει, αλλά με χρόνο και υπομονή, ένα μήνυμα φτάνει στον Μπομπ.
Εκ των υστέρων επιλογή (διατήρηση μόνο των καλών πλαισίων)
Μετά την επιλογή σημαίνει ότι διατηρείτε μόνο τις μετρήσεις που περνούν από ένα φίλτρο (ένα «παράθυρο»). Αυτό μπορεί να κάνει το κρυφό μοτίβο πιο σαφές - αλλά πετάτε τα περισσότερα δεδομένα, επομένως το αποτελεσματικό ποσοστό σταγόνες. Κερδίζετε σαφήνεια, χαλαρά διακίνησηΕίναι μια δίκαιη συναλλαγή αν ο στόχος είναι να αποδειχθεί ότι το αποτέλεσμα υπάρχει.
Αναλογία: Παρακολουθώντας μια βροχή μετεωριτών αλλά μετρώντας μόνο τις πιο φωτεινές ραβδώσεις - βλέπετε το μοτίβο πιο καθαρά, αλλά καταγράφετε λιγότερα συμβάντα ανά ώρα.
Συνθήκες συνέπειας (πώς αποφεύγουμε τα παράδοξα)
Για να διατηρήσουμε τη φυσική λογική και την αιτιώδη ισορροπία, επιβάλλουμε τρία προστατευτικά κιγκλιδώματα:
- Εντοπισμός: οποιοδήποτε εξωτικό αποτέλεσμα είναι περιορισμένος αυστηρά στην κατασκευασμένη περιοχή (το κενό QCT). Έξω, βασιλεύει η κανονική φυσική.
- Μικρότητα: το αποτέλεσμα είναι μικροσκοπικός - αρκετά για να μετρηθούν, όχι αρκετά για να ανατιναχθεί το σύστημα.
- Παγκόσμια προστασία: πιθανότητες και ενεργειακό ισοζύγιο όταν κοιτάτε το ολόκληρο πείραμα. Τοπικές ιδιορρυθμίες, παγκόσμια λογιστική.
Αναλογία: ένα ασφαλές δοκιμαστικό πεδίο: σπινθήρες μπορούν να πεταχτούν μέσα στο κλουβί Faraday, αλλά τίποτα δεν διαρρέει στο δωμάτιο.
[κάντε κλικ για άνοιγμα] Παγκόσμια Γεννημένος κανόνας Διατηρημένο: Οι αποκρίσεις των τοπικών ανιχνευτών ενδέχεται να αποκλίνουν ελαφρώς.
P(i) = |\langle i | \psi \rangle|^2, \quad \sum_i P(i) = 1.
Στην τυπική κβαντομηχανική, αυτός ο κανόνας είναι αυστηρά γραμμικός και διατηρείται καθολικά: η συνολική πιθανότητα σε όλα τα πιθανά αποτελέσματα ισούται με τη μονάδα και καμία λειτουργία (τοπική ή απομακρυσμένη) δεν μπορεί να αλλάξει αυτήν την ομαλοποίηση. Στο πλαίσιο της Αιτιατικής Φυλλωτής Σηματοδότησης (CFS), ωστόσο, διακρίνουμε μεταξύ παγκόσμια διατήρηση και τοπικές αποκλίσεις.
Παγκόσμια προστασία: Η συνολική πιθανότητα, ολοκληρωμένη σε όλες τις φέτες φυλλώματος, παραμένει κανονικοποιημένη:
\int_{\Sigma_t} \sum_i P(i,t),d^3x = 1,
για κάθε παγκόσμιο χρονικό διάστημα \Sigma_t ορίζεται από το διάνυσμα φυλλόπτωσης ου^α.
Τοπικές αποκλίσεις: Μέσα σε ένα ενεργοποιημένο μέσο (όπως το κενό σήραγγας QCT), τα στατιστικά στοιχεία του τοπικού ανιχνευτή μπορούν να παρουσιάσουν μικρές μη γραμμικές μετατοπίσεις στα βάρη πιθανότητας, ενώ ο μέσος όρος του συνόλου εξακολουθεί να υπακούει στον κανόνα Born.
1. Τοπικό μη γραμμικό μοντέλο απόκρισης
Έστω η μη διαταραγμένη πιθανότητα Born να είναι P_0(i) = \operatorname{Tr}(\rho,\Pi_i), όπου \rho είναι ο πίνακας πυκνότητας και \Pi_i = |i\κλίση\κλίση i| είναι προβολείς. Σε ένα ενεργοποιημένο μέσο με ασθενή μη γραμμική σύζευξη \varepsilon, η αποτελεσματική απόκριση του τοπικού ανιχνευτή είναι:
P_{\text{loc}}(i) = \frac{\operatorname{Tr}(\rho,\Pi_i) + \varepsilon,f_i(\rho,\chi)}{\sum_j [\operatorname{Tr}(\rho,\Pi_j) + \varepsilon,f_j(\rho,\chi)]}, \qquad 0<\varepsilon\ll 1.[/latex] Εδώ [latex]f_i(\rho,\chi) είναι ένας μικρός διορθωτικός όρος που προκαλείται από το πεδίο σήματος \χι ή η εξαφανιστική σύζευξη του QCT, και ο παρονομαστής επανακανονικοποιεί τη συνολική πιθανότητα διατήρησης \sum_i P_{\text{loc}}(i) = 1.
2. Παράδειγμα: μέτρηση δύο αποτελεσμάτων (δυαδικός ανιχνευτής)
Θεωρήστε ένα παρατηρήσιμο αποτέλεσμα δύο (π.χ., «αύξηση ρεύματος» έναντι «καμία αύξηση») που μετριέται στην πλευρά του Bob μιας συσκευής QCT. Χωρίς καμία μη γραμμική σύζευξη, P_0(1) = \operatorname{Tr}(\rho,\Pi_1) = p, \quad P_0(0)=1-p. Με ασθενή μη γραμμική σύζευξη και διόρθωση που εξαρτάται από τη φάση f_1 = \άλφα,\sin\φι, f_0=-f_1, η τοπική πιθανότητα γίνεται
P_{\text{loc}}(1) = \frac{p + \varepsilon,\alpha,\sin\phi}{1 + \varepsilon,\alpha,(2p-1)\sin\phi}, \quad P_{\text{loc}}(0)=1-P_{\text{loc}}(1).
Επέκταση σε πρώτη τάξη το \varepsilon:
P_{\text{loc}}(1) περίπου p + \βαρέψιλον, \άλφα, \sin\φ,[1 - p(2p-1)].
Η πιθανότητα τοπικής μέτρησης ταλαντώνεται ελαφρώς με τη φάση σύζευξης \phi (π.χ., διαμόρφωση πόλωσης ή συντονισμός σήραγγας στο QCT). Σε πολλές εκτελέσεις ή όταν ενσωματώνονται συνολικά, αυτές οι αποκλίσεις εξισορροπούνται, αποκαθιστώντας την προσδοκία Born. \langle P_{\text{loc}}(1)\rangle = p.
3. Συνολική (συνολική) αποκατάσταση
Ορίστε τον μέσο όρο του συνόλου σε φέτες φυλλώματος:
\langle P(i) \rangle = \int_{\Sigma_t} P_{\text{loc}}(i, x, t),d^3x.
Εάν οι διορθώσεις f_i ολοκλήρωση στο μηδέν,
\int_{\Sigma_t} f_i(\rho,\chi),d^3x = 0,
τότε ο καθολικός κανόνας Born παραμένει ακριβής:
\sum_i \langle P(i) \rangle = 1.
Έτσι, οι φαινομενικές τοπικές αποκλίσεις είναι στατιστικές κυματισμοί, όχι παραβιάσεις - παρόμοιες με τις διακυμάνσεις που σχετίζονται με τη φάση σε ένα μη γραμμικό οπτικό σύστημα.
4. Φυσική σημασία στο QCT
Σε ένα πείραμα QCT, η τοπική απόκλιση \varepsilon f_i(\rho,\chi) θα μπορούσε να εκδηλωθεί ως θόρυβος συσχετισμένος με πόλωση ή υπερβολικές μετρήσεις σε ανιχνευτές κλίμακας femtosecond. Ωστόσο, σε παγκόσμιο επίπεδο (με μεγαλύτερη ολοκλήρωση), η κανονικοποίηση ισχύει - δεν δημιουργείται ή χάνεται ενέργεια ή πιθανότητα. Επομένως, ο κανόνας Born διατηρείται σε παγκόσμιο επίπεδο, ενώ οι τοπικοί ανιχνευτές ενδέχεται να εμφανίζουν μικρές, αναπαραγώγιμες, εξαρτώμενες από τη φάση αποκλίσεις στους ρυθμούς μέτρησης.
Συνοπτικές εξισώσεις:
Παγκόσμια ομαλοποίηση (κανόνας γεννημένου):
\sum_i P(i) = 1.
Τοπική απόκριση με μικρή μη γραμμική ή χ-εξαρτώμενη απόκλιση:
P_{\text{loc}}(i) = P_0(i) + \varepsilon, \ΔP(i, \chi), \quad \sum_i \ΔP(i, \chi) = 0.
Το παγκόσμιο σύνολο εξακολουθεί να ικανοποιεί:
Σύνοψη ερμηνείας: Οι τοπικοί ανιχνευτές σε μια ενεργοποιημένη περιοχή QCT μπορεί να εμφανίζουν μικρές, συσχετισμένες με τη μεροληψία μετατοπίσεις πιθανότητας, αλλά οι μέσοι όροι του συνόλου των συνόλων διατηρούν ακριβώς τη συνολική πιθανότητα, σύμφωνα με τον κανόνα Born. Αυτή η διάκριση επιτρέπει ασθενείς, ελέγξιμες αποκλίσεις που θα μπορούσαν να χρησιμεύσουν ως εμπειρικά αποτυπώματα μη γραμμικής ή μετα-επιλεγμένης δυναμικής - χωρίς να παραβιάζονται τα βασικά κβαντικά αξιώματα.
Ο κανόνας του Born - ο βασικός κανόνας της κβαντομηχανικής «η πιθανότητα προσθέτει στο 1» - εξακολουθεί να ισχύει παγκοσμίως. Τοπικά, μέσα στο κενό, οι αποκρίσεις του ανιχνευτή μπορούν να είναι ελαφρώς στραβό (αυτό είναι το θέμα), αλλά όταν υπολογίζεις σωστά τον μέσο όρο των πάντων, οι τυπικοί κανόνες παραμένουν άθικτοι. Λυγίζουμε, δεν παραβιάζουμε.
Αναλογία: ένας καθρέφτης-σπίτι που παραμορφώνει την αντανάκλασή σας σε μια γωνία - αλλά το δομικό σχέδιο του κτιρίου δεν έχει αλλάξει.
[κάντε κλικ για άνοιγμα] Προϋπολογισμός σήματος: Διατηρημένη Ποσότητα Q_{\text{sig}} Ικανότητα Επικοινωνίας Ορίων.
Σε ένα ενεργοποιημένο μέσο όπως το Κβαντικό Συζευγμένο Τρανζίστορ (QCT), οι αλληλεπιδράσεις πεδίου μπορούν να ανταλλάξουν πληροφορίες φάσης διαμέσου ενός φράγματος σήραγγας ταχύτερα από την κλασική διάδοση. Ωστόσο, αυτή η ανταλλαγή περιορίζεται από μια διατηρούμενη βαθμωτή ποσότητα που ονομάζεται προϋπολογισμός σήματος, που συμβολίζεται με Q_{\text{sig}}Μετράει τη συνολική ροή συνεκτικού πεδίου - το μέγιστο «πληροφοριακό φορτίο» που μπορεί να ανταλλαχθεί χωρίς να παραβιάζονται οι παγκόσμιοι νόμοι διατήρησης.
Ορίστε την τοπική πυκνότητα ροής σήματος j_{\text{sig}}^a που σχετίζεται με την ανταλλαγή πεδίου με συνοχή φάσης (ανάλογη με μια πιθανότητα ή ένα ρεύμα ενέργειας). Η συνολική διατηρούμενη ποσότητα είναι Q_{\text{sig}} = \int_{\Sigma_t} j_{\text{sig}}^a,u_a,d^3x, όπου \Sigma_t είναι μια υπερεπιφάνεια σταθερού ολικού χρόνου (η φέτα φυλλώματος), u_a είναι η τοπική μονάδα κάθετη σε αυτήν την τομή (το ίδιο πεδίο διανύσματος φυλλόπτωσης που ορίζει το προτιμώμενο πλαίσιο), και j_{\text{sig}}^a υπακούει σε μια εξίσωση συνέχειας \nabla_a j_{\text{sig}}^a = 0. Αυτό υπονοεί \frac{d Q_{\text{sig}}}{dt} = 0, so Q_{\text{sig}} διατηρείται υπό όλες τις τοπικές αλληλεπιδράσεις εντός της ενεργοποιημένης περιοχής.
Φυσικώς, Q_{\text{sig}} ποσοτικοποιεί τη συνολική συνεκτική ενέργεια συσχέτισης ή τη χωρητικότητα φάσης που είναι αποθηκευμένη στο εξαφανιστικό πεδίο σύζευξης μεταξύ κόμβων (Alice και Bob). Δεν είναι ταυτόσημο με το ηλεκτρικό φορτίο ή τον αριθμό φωτονίων. Αντίθετα, μετρά τον ολοκληρωμένο βαθμό αμοιβαίας συνοχής που είναι διαθέσιμος για διαμόρφωση. Οποιαδήποτε διαδικασία επικοινωνίας μπορεί μόνο να αναδιανείμει αυτήν την ποσότητα - ποτέ να μην την αυξήσει.
Η κλασική (Shannon) ικανότητα επικοινωνίας C που επιτυγχάνεται μέσω ενός καναλιού που βασίζεται σε QCT οριοθετείται από μια μονοτονική συνάρτηση του προϋπολογισμού σήματος: C ≤ f(Q_{\text{sig}}), όπου f(\cdot) εξαρτάται από τη γεωμετρία της συσκευής, τον ρυθμό αποσυνοχής και τον θερμικό θόρυβο. Για καθεστώτα μικρού σήματος, γραμμικής απόκρισης, f(Q_{\text{sig}}) περίπου \frac{1}{2N_0},Q_{\text{sig}}^2, όπου Ν_0 είναι η ενεργός φασματική πυκνότητα θορύβου της σύνδεσης σήραγγας, δίνοντας C_{\max} \propto Q_{\text{sig}}^2. Έτσι, μια μεγαλύτερη συνεκτική ροή αποδίδει υψηλότερη δυναμική χωρητικότητα, αλλά μόνο μέχρι το σημείο όπου η αποσυνοχή διακόπτει τη συνέχεια φάσης. Θεωρήστε δύο κόμβους QCT (Alice και Bob) που συνδέονται μόνο με ένα εξαφανιστικό πεδίο σήραγγας. Έστω \Phi_1(t) και \Phi_2(t) να είναι τα στιγμιαία δυναμικά φάσης τους. Ορίστε το συνεκτικό ρεύμα σήματος μέσω του διακένου σύζευξης ως
όπου \κάππα είναι μια σταθερά σύζευξης ανάλογη του συντελεστή σήραγγας φραγμού. Ο ολοκληρωμένος προϋπολογισμός σήματος σε ένα διάστημα συνοχής T_c is
Αυτό αντιπροσωπεύει τη συνολική συσχετισμένη ως προς τη φάση ανταλλαγή μεταξύ της Alice και του Bob εντός του παραθύρου συνοχής και παραμένει σταθερό εάν και οι δύο κόμβοι εξελίσσονται υπό ενιαία ή ασθενώς διαχυτική δυναμική. Έστω I_{\text{sig}}(t) = j_{\text{sig}}(t),A να είναι το μετρήσιμο ρεύμα σήματος μέσω της ενεργού περιοχής A.
Ο στιγμιαίος λόγος σήματος προς θόρυβο είναι \text{SNR}(t) = \frac{I_{\text{sig}}^2(t)}{N_0,B}, όπου B είναι το εύρος ζώνης. Η ενσωμάτωση μέσω του παραθύρου συνοχής δίνει το συνολικό όριο χωρητικότητας
C \le \frac{1}{2B\ln 2}\int_0^{T_c}\frac{I_{\text{sig}}^2(t)}{N_0},dt = \frac{A^2}{2B\ln 2,N_0}\int_0^{T_c} j_{\text{sig}}^2(t),dt.
Σύμφωνα με το θεώρημα του Parseval, αυτό το ολοκλήρωμα είναι ανάλογο με Q_{\text{sig}}^2, δίνοντας C \le k_B,Q_{\text{sig}}^2, όπου k_B είναι μια εμπειρική σταθερά αναλογίας που εξαρτάται από τη γεωμετρία και τη θερμοκρασία. Για ένα αριθμητικό παράδειγμα, ας υποθέσουμε ότι ένα ζεύγος QCT λειτουργεί με σύζευξη φραγμού \κάπα = 10^{-3}, πλάτος συνοχής |\Φ_1| = |\Φ_2| = 1, και χρόνος συνοχής T_c = 10^{-12},\text{s}.
Τότε Q_{\text{sig}} = \kappa \int_0^{T_c} \sin(\Delta\phi),dt \approx \kappa,T_c,\sin\langle\Delta\phi\rangle.
Για μέση υστέρηση φάσης \langle\Delta\phi\rangle = \pi/4, Q_{\text{sig}} περίπου 7.1\times10^{-16},\text{s}.
Με N_0 = 10^{-20},\text{J/Hz} και Β = 10^{12},\text{Hz}, το όριο χωρητικότητας γίνεται C_{\max} περίπου \frac{1}{2B\ln 2}\frac{Q_{\text{sig}}^2}{N_0} περίπου 3 φορές 10^2,\text{bits/s}.
Έτσι, ακόμη και ένας παλμός συνοχής κλίμακας femtosecond θα μπορούσε, κατ' αρχήν, να μεταφέρει μετρήσιμες δομημένες πληροφορίες εντός των ορίων φυσικής διατήρησης.
Εάν υπάρχουν δύο περιοχές σύζευξης παράλληλα, οι συνολικοί προϋπολογισμοί σήματος τους αθροίζονται γραμμικά: Q_{\text{sig,tot}} = Q_{\text{sig}}^{(1)} + Q_{\text{sig}}^{(2)}, αλλά οι αντίστοιχες χωρητικότητες αθροίζονται υπογραμμικά λόγω παρεμβολών: C_{\text{συνολικά}} ≤ f(Q_{\text{sig,συνολικά}}) < f(Q_{\text{sig}}^{(1)}) + f(Q_{\text{sig}}^{(2)}).[/latex] Αυτό εκφράζει την πεπερασμένη ικανότητα της συνοχής: η συνοχή μπορεί να μοιραστεί αλλά όχι να ενισχυθεί ελεύθερα. Συνοψίζοντας, [latex]Q_{\text{sig}} είναι ένα διατηρημένο βαθμωτό που αντιπροσωπεύει τη συνολική συνεκτική ροή πεδίου μέσω του ενεργοποιημένου μέσου. Ορίζει τον μέγιστο προϋπολογισμό επικοινωνίας του συστήματος, C ≤ f(Q_{\text{sig}}), διασφαλίζοντας ότι οποιαδήποτε αύξηση της μετρήσιμης χωρητικότητας θα αντληθεί από τη διαθέσιμη Q_{\text{sig}}Η αρχή εγγυάται την αιτιότητα και τη θερμοδυναμική συνέπεια ακόμη και για υπερφωτεινή σύζευξη φάσεων: η ανταλλαγή πληροφοριών παραμένει οριοθετημένη από μια διατηρημένη ποσότητα σήματος.
Επεξεργαζόμαστε τα διαθέσιμα συνοχή (το εύτακτο μέρος του κοντινού πεδίου στο κενό) σαν ένα προϋπολογισμός. Μπορείτε να διανέμω εκ νέου για να στείλεις ένα μήνυμα, αλλά εσύ δεν μπορεί να δημιουργήσει περισσότερα από το τίποτα. Περισσότερος προϋπολογισμός → δυνητικά υψηλότερη αξιόπιστη τιμή, μέχρι ο θόρυβος και η θερμότητα να πουν «σταμάτα».
Αναλογία: μια μπαταρία για έναν εξαιρετικά λεπτό δείκτη λέιζερ: μπορείτε να αναβοσβήνετε έναν κωδικό, αλλά ο συνολικός αριθμός αναβοσβησιμάτων περιορίζεται από την μπαταρία.
[κάντε κλικ για άνοιγμα] Περιορισμένη Μη ΓραμμικότηταΠαθολογίες που αποφεύγονται με περιορισμό + ενεργειακά όρια.
Σε μη γραμμικά ή μετα-επιλεγμένα κβαντικά συστήματα, η απεριόριστη ανατροφοδότηση μεταξύ κατάστασης και μέτρησης μπορεί εύκολα να οδηγήσει σε παράδοξα: υπερφωτεινή σηματοδότηση, παραβίαση του κανόνα Born ή ακόμη και λογικές ασυνέπειες όπως κλειστοί αιτιώδεις βρόχοι. Για να παραμείνει φυσικά συνεπής, οποιαδήποτε απόκλιση από τη γραμμική κβαντική εξέλιξη πρέπει να είναι αυστηρά περιορισμένος - εντοπισμένο εντός μιας πεπερασμένης, ενεργειακά περιορισμένης περιοχής του χωροχρόνου και συνδεδεμένο με το εξωτερικό περιβάλλον μόνο μέσω καναλιών που διατηρούν την παγκόσμια μοναδιαιότητα. Το Κβαντικά Συζευγμένο Τρανζίστορ (QCT) παρέχει ένα τέτοιο φυσικό όριο. Ο μη γραμμικός όρος αναδύεται μόνο εντός του ενεργοποιημένο μέσο - το διάκενο σήραγγας ή η περιοχή χ-πεδίου - όπου η εξαφανιστική σύζευξη φάσης και η Αρνητική Διαφορική Αντίσταση (NDR) επιτρέπουν ασθενή αυτο-αλληλεπίδραση. Εκτός αυτής της ζώνης, η τυπική γραμμική κβαντομηχανική ισχύει ακριβώς.
Τυπικά, ας γραφτεί ο πλήρης τελεστής εξέλιξης συστήματος ως U(t) = T exp![-hbar(H_0 + nl,H_{NL}),dt], όπου Η_0 είναι η τυπική Ερμιτιανή Χαμιλτονιανή, H_{\text{NL}} είναι μια φραγμένη μη γραμμική συνεισφορά, και \βαρέψιλον \ll 1 είναι μια παράμετρος ενεργοποίησης που μηδενίζεται εκτός της περιοχής QCT. Η συνθήκη περιορισμού είναι \operatorname{supp}(H_{\text{NL}}) \subseteq \Omega_{\text{QCT}}, που σημαίνει ότι η μη γραμμική αλληλεπίδραση περιορίζεται χωρικά στο ενεργοποιημένο μέσο \Ωμέγα_{\text{QCT}}Η καθολική μοναδικότητα διατηρείται εάν ο μεταθέτης [H_{\text{NL}},H_0] έχει συμπαγή υποστήριξη και μη γραμμική ενεργειακή πυκνότητα
\mathcal{E} {\text{NL}} = \langle\psi|H {\text{NL}}|\psi\rangleικανοποιεί
\mathcal{E} {\text{NL}} \le \delta E {\text{th}},όπου \δέλτα E_{\text{th}} είναι η τοπική κλίμακα θερμικής διακύμανσης. Αυτό διασφαλίζει ότι η μη γραμμική ανάδραση δεν μπορεί να αυτοενισχυθεί πέρα από τα φυσικά όρια θορύβου.
Λειτουργικά, ο περιορισμός υπονοεί ότι ο χάρτης \Φι: \ρο \μάπστο \ρο' είναι ασθενώς μη γραμμικό μόνο εντός του υποχώρου με δυνατότητα χ
\mathcal{H} {\chi},ενώ παραμένει εντελώς θετικό και διατηρεί ίχνη (CPTP) στο συμπλήρωμα. Μαθηματικά,
\Phi = \Phi {\text{CPTP}} \oplus (\Phi_{\text{CPTP}} + \varepsilon \mathcal{N}),μαζί σου, \mathcal{N} που αντιπροσωπεύει την περιορισμένη μη γραμμική διόρθωση. Επειδή \varepsilon \rightarrow 0 Στο όριο του QCT, καμία μη γραμμικότητα δεν διαδίδεται πέρα από το κενό. Αυτό αποτρέπει τις καθολικές ασυνέπειες και επιβάλλει το αιτιώδες κλείσιμο: τα φαινόμενα υπερφωτεινής φάσης μπορεί να υπάρχουν εντός της τοπικής φύλλωσης, αλλά δεν μπορούν να σχηματίσουν κλειστούς βρόχους σηματοδότησης ή να διαδοθούν αυθαίρετα.
Θερμοδυναμικά, ο περιορισμός της μη γραμμικότητας διασφαλίζει ότι η εξαγωγή ενέργειας από το κενό είναι αδύνατη. Η ενεργή περιοχή NDR λειτουργεί ως ελεγχόμενο στοιχείο ανάδρασης που μπορεί να ενισχύσει τα εξασθενημένα πεδία, αλλά πάντα εντός του περιορισμού. P_{\text{έξω}} ≤ P_{\text{είσαι}} + \Δέλτα E_{\text{αποθηκεύεται}}Οποιοδήποτε παροδικό κέρδος αντισταθμίζεται από την τοπική αποθήκευση πεδίου, διατηρώντας τη συνολική ενεργειακή ισορροπία. Έτσι, το σύστημα συμπεριφέρεται ως ένας μη γραμμικός συντονιστής που περικλείεται σε ένα συντηρητικό όριο.
Στο πλαίσιο της Αιτιατικής Φυλλωτής Σηματοδότησης (CFS), αυτός ο χωρικός και ενεργειακός περιορισμός εγγυάται σταθερότητα: η μη γραμμική δυναμική τροποποιεί τις τοπικές στατιστικές χωρίς να μεταβάλλει την παγκόσμια μοναδιαιότητα. Η QCT γίνεται μια μη γραμμικό νησί με ενεργειακά όρια ενσωματωμένο σε ένα γραμμικό κβαντικό συνεχές.
Παθολογίες όπως η ανεξέλεγκτη ενίσχυση, ο υπερντετερμινισμός ή η μη αιτιώδης ανάδραση αποκλείονται αυτόματα επειδή ο μη γραμμικός τομέας είναι πεπερασμένος, συζευγμένος με διασπορά και επανακανονικοποιημένος καθολικά. Στην ουσία, το QCT λειτουργεί ως ένα sandbox όπου μπορεί να υπάρχει περιορισμένη μη γραμμικότητα, ελέγξιμη αλλά ασφαλής καραντίνα εντός των κανόνων της κβαντικής θερμοδυναμικής.
Το χάσμα h-BN του QCT λειτουργεί σαν ένα Κλουβί Faraday για κβαντική παραδοξότητα - ένα μικροσκοπικό sandbox όπου οι συνήθεις κανόνες μπορούν να παρακαμφθούν με ασφάλεια χωρίς να παραβιαστούν. Μέσα σε αυτήν την σφραγισμένη ζώνη, η συσκευή μπορεί να ενισχύσει και να ανακυκλώσει ενέργεια ακριβώς όσο χρειάζεται για να αποκαλύψει αμυδρά υπερφωτεινά μοτίβα, αλλά αυστηρά θερμικά και ενεργειακά όρια την εμποδίζουν να εξαφανιστεί.
Αναλογία: Είναι σαν να χτίζεις ένα ενισχυτής με τείχος προστασίας: μπορεί να ψιθυρίζει στο κενό, αλλά ποτέ δεν καταπατά τους νόμους της φυσικής που το περιέχουν.
[κάντε κλικ για άνοιγμα] Θερμοπεριοχές (Κέρδος έναντι Θερμοκρασίας Θορύβου)
Κάθε ενεργή κβαντική συσκευή περιορίζεται τελικά από θερμοδυναμική συνέπεια. Ακόμα και όταν το Κβαντικό Συζευγμένο Τρανζίστορ (QCT) λειτουργεί σε μη γραμμικό ή Αρνητικό Διαφορικό Αντίστασης (NDR), το συνολικό του κέρδος δεν μπορεί να υπερβεί το όριο που ορίζεται από την ενεργό θερμοκρασία θορύβου και τον διαθέσιμο προϋπολογισμό σήματος. Θερμοδεμένος εκφράζει αυτό το όριο: η ενίσχυση και η μεταφορά συνοχής στο ενεργοποιημένο μέσο πρέπει να υπακούουν στην αρχή της διακύμανσης-απαλλαγής, διασφαλίζοντας ότι καμία διαμόρφωση της συσκευής δεν μπορεί να εξαγάγει καθαρή ελεύθερη ενέργεια ή να παραβιάσει τον Δεύτερο Νόμο.
Σε ισορροπία, η φασματική πυκνότητα ισχύος των διακυμάνσεων κατά μήκος του κενού σήραγγας είναι S_V(f) = 4k_B T_{\text{eff}} R_{\text{eq}}(f), όπου T_{\text{eff}} είναι η ενεργός θερμοκρασία της συζευγμένης επαφής και R_{\text{eq}}(f) είναι η δυναμική αντίσταση, η οποία μπορεί να γίνει αρνητική υπό πόλωση NDR. Όταν το QCT παρέχει κέρδος μικρού σήματος G(f), το θεώρημα διακύμανσης-απαγωγής απαιτεί το γινόμενο του κέρδους και της θερμοκρασίας θορύβου να παραμένει φραγμένο: G(f) T_{\text{eff}} \ge T_0, όπου T_0 είναι η φυσική θερμοκρασία του περιβάλλοντος. Αυτό διασφαλίζει ότι οποιαδήποτε τοπική ενίσχυση εισάγει απαραίτητα αντισταθμιστικό θόρυβο, διατηρώντας την ισορροπία εντροπίας μη αρνητική.
Το κβαντικό ανάλογο αυτού του περιορισμού προκύπτει από τις σχέσεις μεταγωγής των τελεστών πεδίου. Για κάθε ενισχυτή που λειτουργεί σε μποζονικούς τρόπους \hat a_{\mathrm{in}} και \hat a_{\mathrm{out}}, η κανονική μετατροπή πρέπει να διατηρηθεί, δηλαδή
[,\hat a_{\mathrm{out}},,\hat a_{\mathrm{out}}^{\dagger},]=1.
Ένα τυπικό μοντέλο εισόδου-εξόδου που δεν είναι ευαίσθητο στη φάση είναι
\hat a_{\mathrm{out}}=\sqrt{G},\hat a_{\mathrm{in}}+\sqrt{G-1},\hat b_{\mathrm{in}}^{\dagger},\qquad [,\hat b_{\mathrm{in}},\hat b_{\mathrm{in},\hat b_{\mathrm{in}
πράγμα που συνεπάγεται ελάχιστο πρόσθετο θόρυβο.
Στο QCT, αυτός ο θόρυβος αντιστοιχεί στη στοχαστική συνιστώσα του ρεύματος σήραγγας που προκαλείται από θερμικές και κβαντικές διακυμάνσεις του εξαφανιζόμενου πεδίου. Η αποτελεσματική αντιστάθμιση κέρδους-θορύβου μπορεί να γραφτεί ως G_{\text{QCT}} = 1 + \frac{P_{\text{έξω}} - P_{\text{είσαι}}}{k_B T_{\text{αποτελέσματα}} B}, υποτάσσω P_{\text{έξω}} ≤ P_{\text{είσαι}} + k_B T_{\text{απο}} B, όπου B είναι το εύρος ζώνης. Αυτή η ανισότητα εκφράζει το θερμοδυναμικό ανώτατο όριο στην συνεκτική ενίσχυση.
Στην πράξη, καθώς αυξάνεται η πόλωση κατά μήκος του φράγματος h-BN, η περιοχή NDR επιτρέπει την επανέγχυση ενέργειας στην εξαφανιστική λειτουργία, ενισχύοντας αποτελεσματικά το κοντινό πεδίο. Ωστόσο, αυτό το κέρδος είναι αυτοπεριοριζόμενο: μόλις η τοπική θερμοκρασία θορύβου αυξηθεί στο T_{\text{eff}} = T_0 + ΔT_{\text{NDR}}, το σύστημα φτάνει σε θερμική σταθερή κατάσταση. Η περαιτέρω αύξηση της πόλωσης διαχέει την επιπλέον ενέργεια ως θερμότητα αντί να αυξάνει τη συνοχή. Ως εκ τούτου, το θερμικό επίπεδο θορύβου λειτουργεί ως φυσικό φρένο, σταθεροποιώντας το σύστημα έναντι της αλόγιστης ενίσχυσης.
Το Θερμικό Όριο μπορεί επομένως να συνοψιστεί ως ένας νόμος διατήρησης που συνδέει την απόκτηση πληροφοριών, την ενεργειακή εισροή και την παραγωγή εντροπίας: Δέλτα I ≤ Δέλτα E}{k_B T_{\text{eff}} ln 2}. Αυτή η ανισότητα ορίζει την τελική απόδοση οποιουδήποτε καναλιού επικοινωνίας που βασίζεται σε QCT ή πειράματος αιτιώδους-φολιδωτής σηματοδότησης: ο ρυθμός πληροφοριών που επιτυγχάνεται ανά μονάδα ενεργειακής δαπάνης δεν μπορεί να υπερβεί το κόστος εντροπίας για τη διατήρηση της συνοχής.
Από μια ευρύτερη οπτική γωνία, το Thermo Bound είναι το θερμικό αντίστοιχο του περιορισμού προϋπολογισμού σήματος. Q_{\text{sig}} οριοθετεί τη συνολική συνεκτική ροή, T_{\text{eff}} περιορίζει την χρησιμοποιήσιμη ενίσχυση εντός αυτής της ροής. Μαζί, ορίζουν το λειτουργικό παράθυρο του QCT ως ένα κβαντικά συντονισμένο αλλά θερμοδυναμικά κλειστό σύστημα. Δεν δημιουργείται ούτε χάνεται ενέργεια πέρα από την επιτρεπόμενη ανταλλαγή με το περιβάλλον και η συνολική μεταβολή της εντροπίας παραμένει μη αρνητική: \frac{dS_{\text{tot}}}{dt} = \frac{P_{\text{in}} - P_{\text{out}}}{T_0} \ge 0.
Στην ουσία, το Thermo Bound διασφαλίζει ότι το QCT λειτουργεί ως θερμοδυναμικά συμβατός κβαντικός ενισχυτής - ικανό για κέρδος συνεκτικής φάσης και υπερφωτεινή σύζευξη εντός της ενεργοποιημένης περιοχής του, αλλά πάντα περιορισμένο από την υποκείμενη ισορροπία ενέργειας-εντροπίας που διατηρεί την παγκόσμια αιτιότητα και τον φυσικό νόμο.
Αν προσπαθήσετε να ενισχύσετε το κοντινό πεδίο στο κενό, αυξάνετε επίσης την έντασή του. αποτελεσματική θερμοκρασία θορύβουΥπάρχει ένα συμβιβασμός: περισσότερο κέρδος σημαίνει περισσότερος θόρυβος. Η φύση επιβάλλει αυτήν την ισορροπία, ώστε εσείς δεν μπορεί να αποκτήστε δωρεάν ενέργεια ή απεριόριστη, κρυστάλλινη ενίσχυση.
Αναλογία: Δυναμώνοντας τον ενισχυτή κιθάρας: πιο δυνατό σήμα, αλλά και περισσότερο σφύριγμα. Κάποια στιγμή, η επιπλέον ένταση απλώς προσθέτει θόρυβο και θερμότητα.
[κάντε κλικ για άνοιγμα] Ελάχιστο Μοντέλο: Δυναμική Μη Γραμμικού Ανιχνευτή/Ενισχυτή σε Ενεργοποιημένα Μέσα
Σε ενεργοποιημένες περιοχές όπως το φράγμα σήραγγας QCT, υποθέτουμε την παρουσία μιας ασθενούς, εξαρτώμενης από την κατάσταση μη γραμμικότητας στον χάρτη μέτρησης ή ενίσχυσης. Αυτός ο χάρτης, που συμβολίζεται με Ν_{\chi}, λειτουργεί στον τοπικό πίνακα πυκνότητας \rho του υποσυστήματος που συνδέεται με το πεδίο σήματος \χιΔιατηρεί την ολική πιθανότητα (διατήρηση ιχνών) αλλά εισάγει μια ελεγχόμενη μη γραμμικότητα επαρκή για να αποδώσει μια πεπερασμένη, αν και μικροσκοπική, κλασική χωρητικότητα.
1. Ορισμός
N_{\chi}(\rho) = \frac{A_{\chi} \rho A_{\chi}^{\dagger}}{\mathrm{Tr}(A_{\chi} \rho A_{\chi}^{\dagger})},
όπου A_{\chi} = I + εψιλον, F(\rho, \chi) είναι ένας μη γραμμικός τελεστής που εξαρτάται ασθενώς από το πεδίο σήματος \χι και στην τρέχουσα κατάσταση του συστήματος \rhoΗ μικρή παράμετρος \έψιλον \ll 1 ελέγχει τον βαθμό μη γραμμικότητας.
Η κανονικοποίηση στον παρονομαστή επιβάλλει \mathrm{Tr}[N_{\chi}(\rho)] = 1, διασφαλίζοντας ότι ο χάρτης διατηρεί τα ίχνη του και είναι φυσικά συνεπής.
2. Γραμμικό Όριο
Όταν \έψιλον = 0, το μοντέλο ανάγεται σε τυπική κβαντική μέτρηση:
N_{\chi}(\rho) \to \rho' = \frac{M \rho M^{\dagger}}{\mathrm{Tr}(M \rho M^{\dagger})},
όπου M είναι ο τελεστής μέτρησης (στοιχείο POVM).
Έτσι, το μη γραμμικό μοντέλο είναι μια ελάχιστη επέκταση της τυπικής κβαντομηχανικής.
3. Αποτελεσματική Δυναμική
Για ασθενή μη γραμμικότητα, ο χάρτης προκαλεί μια αποτελεσματική εξίσωση εξέλιξης:
\dot{\rho} = -\frac{i}{\hbar}[H, \rho] + \epsilon, \mathcal{L} {\chi}[\rho],όπου
\mathcal{L} {\chi}[\rho]αντιπροσωπεύει μια μη γραμμική συναρτησιακή σύνδεση της κατάστασης του συστήματος με το πεδίο σήματος.
Αυτός ο όρος μπορεί να μοντελοποιηθεί φαινομενολογικά ως εξής:
\mathcal{L}_{\chi}[\rho] = f(\chi),(\rho^2 - \rho,\mathrm{Tr}[\rho^2]),
εισάγοντας κέρδος ή εξασθένηση που εξαρτάται από την κατάσταση και η οποία μηδενίζεται για καθαρές καταστάσεις (\rho^2 = \rho).
4. Ικανότητα Πληροφόρησης
Το βασικό αποτέλεσμα είναι ότι η μετα-επιλεγμένη ή μη γραμμική ανίχνευση μπορεί να αποδώσει μια μικρή αλλά πεπερασμένη κλασική χωρητικότητα C_{\mathrm{eff}} σε αυτό που διαφορετικά θα ήταν ένα κανάλι μόνο για διεμπλοκή (χωρίς σηματοδότηση):
C_{\mathrm{eff}} \approx p_{W}, C,
όπου p_{W} είναι η πιθανότητα επιτυχίας του μη γραμμικού παραθύρου μετά την επιλογή, και C είναι η χωρητικότητα ενός ιδανικού καναλιού σηματοδότησης.
Αυτό αντιστοιχεί σε μια μικροσκοπική αλλά μετρήσιμη απόκλιση από την αυστηρή συμπεριφορά μη επικοινωνίας σε ενεργοποιημένα μέσα:
C_{\mathrm{eff}} > 0, \qquad C_{\mathrm{eff}} \ll C_{\mathrm{κλασικό}}.5. Φυσικό παράδειγμα: Σύνδεσμος φραγμού QCT
Σε ένα κβαντικό συζευγμένο τρανζίστορ, τα δύο στρώματα γραφενίου λειτουργούν ως τοπικά συνεκτικοί ανιχνευτές συνδεδεμένοι μέσω ενός κβαντικού φραγμού.
Το ενεργό πεδίο σήματος \παιδάκι) αντιπροσωπεύει το δυναμικό εξαφανιστικής φάσης στην περιοχή σήραγγας h-BN.
Η μη γραμμικότητα εισέρχεται μέσω της διαφάνειας του φράγματος που εξαρτάται από την τάση:
T_{\chi}(V) = T_{0} \exp[-\alpha (1 - \beta V + \epsilon, \Phi_{\chi}(\rho))],
όπου \Φι_{\χι}(\ρο) είναι ένας ασθενής όρος ανάδρασης που συνδέει τη συνοχή της τοπικής κυματοσυνάρτησης με την κατάσταση του πεδίου.
Μια τέτοια ανατροφοδότηση τροποποιεί την πιθανότητα σήραγγας μη τοπικά, αλλά διατηρεί την καθολική μοναδιαιότητα.
6. Διατήρηση και Σταθερότητα
Για να αποφευχθεί η ασύμμετρη ενίσχυση, ο μη γραμμικός όρος ικανοποιεί έναν περιορισμό διατήρησης:
\mathrm{Tr}[\rho,\mathcal{L}_{\chi}[\rho]] = 0,
διασφαλίζοντας ότι η συνολική πιθανότητα και ενέργεια παραμένουν σταθερές πρώτης τάξης \έψιλο.
Αυτό διατηρεί τη δυναμική αυτοσυνεπή και οριοθετημένη - αποφεύγοντας τα υπερφωτεινά παράδοξα, επιτρέποντας παράλληλα τη μη παρατηρήσιμη, συνεκτική μεταφορά σήματος.
7. Ερμηνεία
Το αποτέλεσμα είναι α ελάχιστα τροποποιημένος κβαντικός κανόνας:
Η απόκριση του ανιχνευτή είναι ελαφρώς μη γραμμική και εξαρτώμενη από την κατάσταση, δημιουργώντας μια μικρή απόκλιση από το αυστηρό θεώρημα μη επικοινωνίας, διατηρώντας παράλληλα την κανονικοποίηση του κανόνα Born καθολικά.
Σε ενεργοποιημένες περιοχές (π.χ., πεδία φραγμού h-BN, κυκλώματα σύμπτωσης μετά την επιλογή), η αλληλεπίδραση συμπεριφέρεται σαν οι πληροφορίες φάσης να μπορούν να διαπεράσουν το κβαντικό κενό - μεταφέροντας ένα μικροσκοπικό, πεπερασμένο κλασικό σήμα διαμέσου του χωρικού διαχωρισμού, χωρίς να διασπάται η μοναδιότητα ή η παγκόσμια αιτιότητα.
Είμαστε δεν ξαναγράφοντας την κβαντομηχανική παντού. Προσθέτουμε ένα μικροσκοπική, εξαρτώμενη από την κατάσταση συστροφή στο πώς αντιδρά ο ανιχνευτής/ενισχυτής μέσα στο κενό - αρκετά ώστε να αφήσει ένα αμυδρό μοτίβο να επικαλύψει τον θόρυβο. Έξω από το κενό, όλα είναι συνηθισμένα και γραμμικά. Στο εσωτερικό, η απόκριση είναι ελαφρώς με επίγνωση του πλαισίου (αυτό είναι το «μη γραμμικό» μέρος), και το διατηρούμε οριοθετημένο οπότε τίποτα δεν ξεφεύγει.
Αναλογία: ένα μικρόφωνο με έναν διακριτικό ενσωματωμένο συμπιεστή που ενεργοποιείται μόνο σε ένα μικροσκοπικό σημείο ευαισθησίας - τις περισσότερες φορές είναι διαφανές, αλλά σε αυτό το σημείο διαμορφώνει το σήμα αρκετά ώστε να ακουστεί.
4. Πειραματικές προβλέψεις
- Ήπια ανισοτροπία πλαισίου: η ταχύτητα του σήματος εξαρτάται από την ευθυγράμμιση με uᵃ
- Φθίνουσα → πολλαπλασιαστική μετατροπή υπό διαμόρφωση πόλωσης QCT
- Ελεγχόμενη Παραβίαση ορίου Τσιρέλσον
- Καθυστέρηση κλιμάκωσης με πόλωση σύνδεσης, όχι πάχος φραγμού
5. Πρωτόκολλα Δοκιμών
- Διεργαστηριακή εξέταση QCT: Η διαμόρφωση πόλωσης στον κόμβο Α παράγει συσχετισμένη απόκριση στον κόμβο Β έξω από τον κώνο φωτός.
- Αλλαγή κινούμενου πλαισίου: Επαναλαμβάνεται σε σχετική κίνηση για να ελεγχθεί η ευθυγράμμιση του προτιμώμενου πλαισίου.
- Φευγαλέα Έγχυση: Κυματοδηγός κάτω από την αποκοπή συνδεδεμένος στο κενό QCT για την ανίχνευση ανάκτησης με διαμόρφωση φάσης.
6. Ο ρόλος του QCT
Η διοχέτευση femtosecond του QCT και η συμπεριφορά NDR δημιουργούν μια περιορισμένη μη γραμμικότητα απαραίτητη για ελεγχόμενη υπερφωτεινή συνοχή. Η αιτιότητα διατηρείται μέσω του περιορισμού χωρίς βρόχο, διασφαλίζοντας την παγκόσμια τάξη.

Συνοψίζοντας: Το CFS διατηρεί τη σχετικότητα σχεδόν παντού, ενώ επιτρέπει έναν δομημένο κώνο σήματος ενεργό μόνο σε συγκεκριμένα κβαντικά μέσα όπως το QCT. Αυτό το πλαίσιο εισάγει ελέγξιμες προβλέψεις για υπερφωτεινή αλλά αιτιωδώς συνεπή επικοινωνία.
Αυτό το άρθρο είναι μέρος μιας σειράς, που σχετίζονται όλα με μια ανεξήγητη παρατήρηση που είχα το 1986 στην Ιρλανδία:
- UFO Πάνω από τον Κόλπο του Γκάλγουεϊ Κεφάλαιο 1: Η Συνάντηση στο Σόλθιλ του 1986
- Η αναφορά για τα μαύρα UFOΠρίγκιπας Κάρολος, ένα τζάμπο τζετ και μια νύχτα εναέριων μυστηρίων
- UFO πάνω από τον κόλπο Galway Κεφάλαιο 2: Μέιντεϊ από ένα συντριμμένο UFO
- UFO πάνω από τον κόλπο Galway Κεφάλαιο 3: Ο Ιρλανδός Tuatha Dé Danann ως Κοσμικοί Επισκέπτες
- UFO Πάνω από τον Κόλπο του Γκάλγουεϊ Κεφάλαιο 4: Αντίστροφη Μηχανική Το Κβαντικό Συνδεδεμένο Τρανζίστορ
- Το Κβαντικό Συζευγμένο Τρανζίστορ (QCT): Ενισχύοντας το Κενό
- Μπορούν οι πληροφορίες να ταξιδέψουν πιο γρήγορα από το φως; - Χωρίς να σπάσουμε τη Φυσική;