🕔 Tiempo estimado de lectura: 32 minutos
La lógica de la señalización causal-foliada
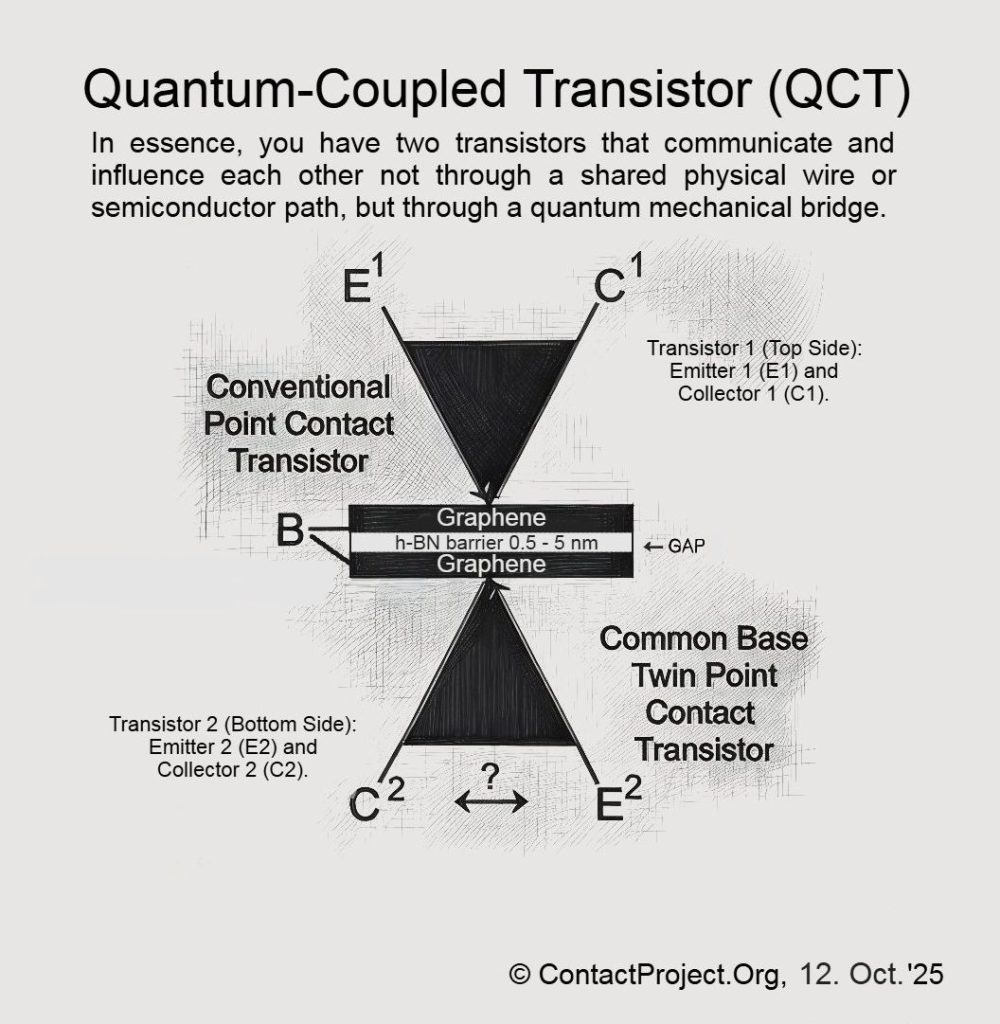
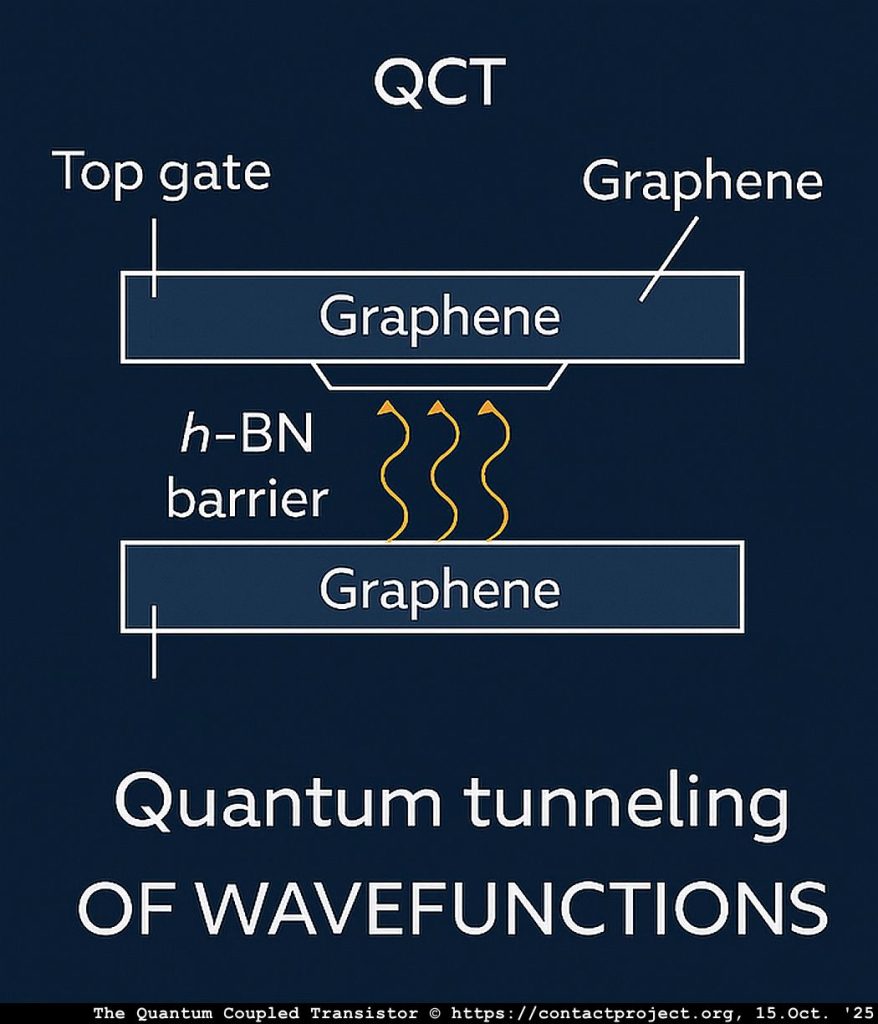
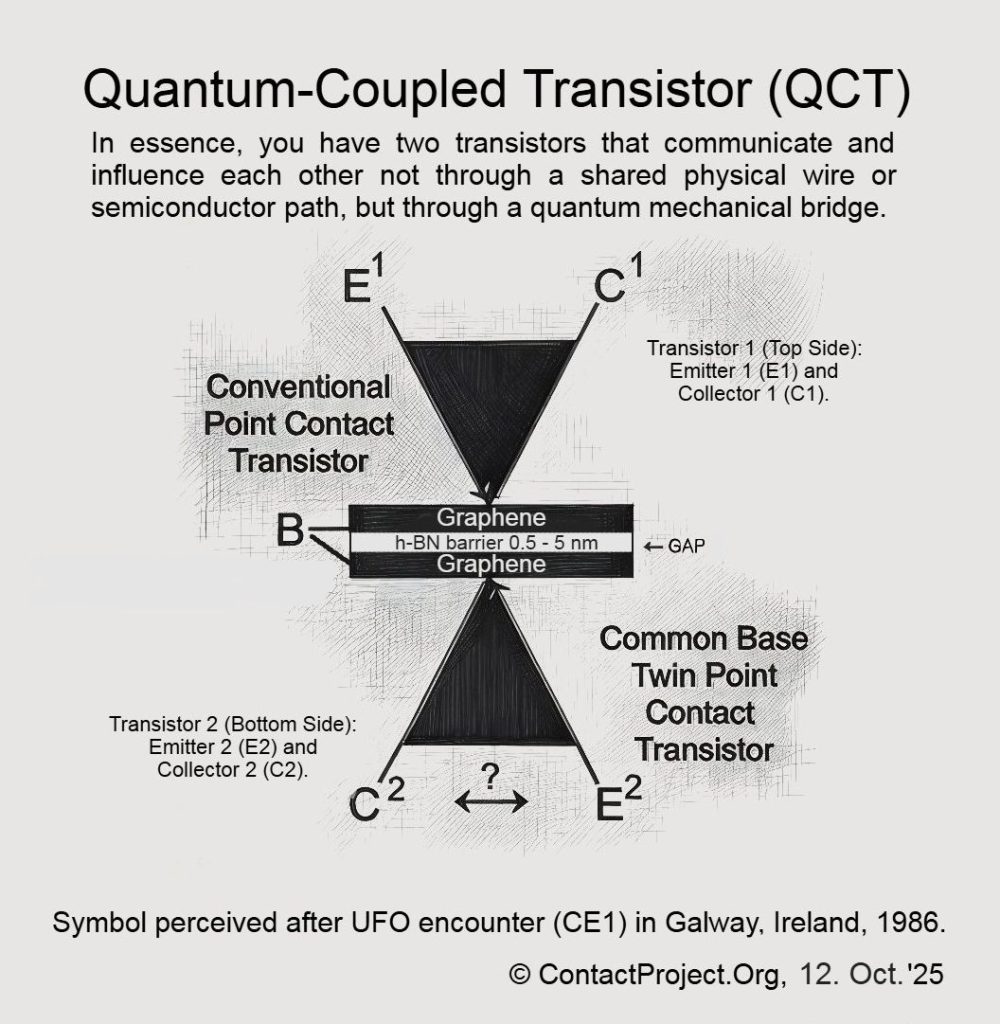
La teoría de Señalización causal-foliada (CFS) Propone que el tiempo contiene capas ocultas que permiten una coherencia limitada, más rápida que la luz, entre sistemas cuánticos. Los investigadores podrían pronto utilizar la Transistor acoplado cuántico (QCT) – un nanodispositivo de grafeno dual – para probar estos efectos directamente y determinar si pueden ocurrir sin romper las leyes conocidas de la física.
En esencia, el CFS plantea una pregunta provocadora: ¿Qué sucedería si ciertos tipos de ondas, como las de campo evanescente o cercano, pudieran compartir información de fase más rápido que la luz y aún así preservar la causalidad?
De ser así, el espacio-tiempo podría no ser perfectamente uniforme. Podría contener una estructura interna sutil: una «capa» de tiempo, donde la información se adelanta ligeramente dentro de cada capa, pero permanece constante en todo el conjunto.

Desde esta perspectiva, el universo se despliega como las páginas de un vasto libro cósmico: cada página se abre en perfecto orden, aunque algunas avancen un poco más rápido que otras. El CFS ofrece una visión refinada de la relatividad, que permite una coherencia superlumínica estructurada, manteniendo intacta la relación de causa y efecto.
Parte II. Señalización Causal-Foliada (SFC)
- Axiomas fundamentales
- Cinemática y dinámica
- Reglas cuánticas y conservación
- Predicciones experimentales
- Protocolos de prueba
- Papel del QCT
1. Axiomas fundamentales
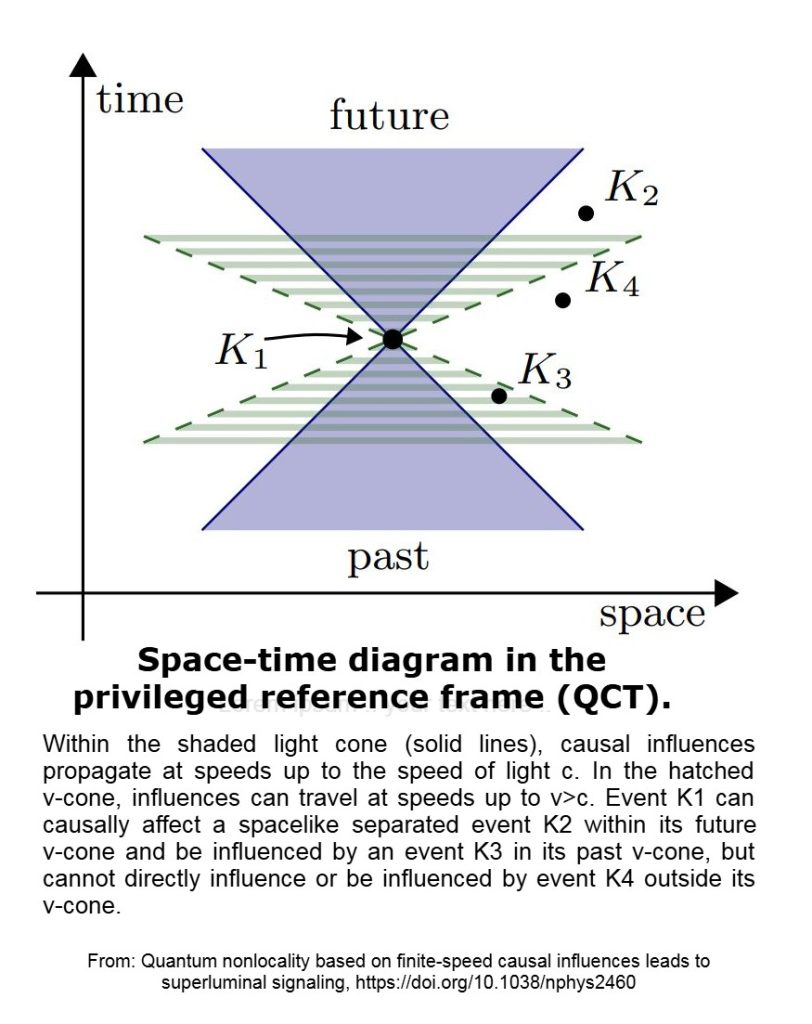
- Foliación temporal global: El espacio-tiempo posee una división global preferida (tiempo cósmico, definido por un vector temporal). uᵃ). Todas las señales, luminales y superluminales, están ordenadas por esta foliación.
- Cono de señal agrandado: Más allá del cono de luz, existe un “cono de señal” más amplio para medios o campos específicos (χ).
- Protección cronológica: Los bucles de señales cerrados están prohibidos dinámicamente por restricciones de solubilidad.
- Localidad operativa: Los experimentos estándar permanecen invariantes respecto de Lorentz; las desviaciones ocurren únicamente dentro de los medios habilitados.
2. Cinemática y dinámica
- Marco preferido: Alineado aproximadamente con el marco de descanso CMB.
- Campo de señal (χ): Se acopla débilmente a los portadores de EM, ampliando el cono causal.
- Características superlumínicas: EDP en medios habilitados exhiben propagación fuera del cono de luz g.
- Restricción sin bucle: Las condiciones integrales evitan bucles causales que disminuyen en el tiempo.
3. Reglas cuánticas y conservación
Construimos una pequeña región (la brecha QCT) donde los campos cercanos cuánticos se pueden moldear suavemente para que un campo más rápido que la luz, apenas detectable, patrón aparece en datos que de otro modo serían aleatorios: lo suficientemente pequeños para mantener la física segura, lo suficientemente claros para probarlos en el laboratorio.

Si la declaración compacta anterior tiene sentido para usted, entonces puede ampliar la línea roja. Reglas cuánticas a continuación, haciendo clic en los triángulos negros ▶, para obtener una discusión MÁS detallada.
Para el público general, cada sección incluye una breve explicación (sin matemáticas) seguida de una analogía. Aunque la mayoría de la gente nunca habrá oído hablar de... teorema de no comunicación (que prohíbe la comunicación más rápida que la luz… por entrelazamiento), se coloca aquí de forma destacada debido a su importancia fundamental y porque controlado relajación de esa regla se explora aquí.
[haga clic para abrir] Teorema de no comunicación relajado: En medios habilitados, la dinámica no lineal/post-seleccionada permite una capacidad clásica minúscula > 0.
Reclamación (operativa):
En una medio habilitado (por ejemplo, una brecha QCT que actúa como campo cercano habilitado por χ), una no linealidad débil y localizada or postselección explícita puede producir un capacidad clásica pequeña pero finita C>0 entre partes separadas espacialmente sin violar la unitaridad global ni la regla de Born.
Configuración
Asegúrate de que ρAB ser un estado bipartito compartido por Alice y Bob. En mecánica cuántica estándar con local Mapas CPTP y no Después de la selección, el estado reducido de Bob es independiente de la elección de Alice:
ρB′=TrA[(ΦA⊗IB)(ρAB)]=ρB, (sin señalización)
En una habilitada Región QCT, modelo de la operación controlada de Alice como una débilmente no lineal perturbación de una Mapa CPTP:
ΦA(V)(⋅)=ΛA(⋅)+ε\mathcal{N}_A^{(V)}[⋅], 0<ε≪1,[/latex] donde [latex]V es el control de Alice (por ejemplo, sesgo entre capas), La es CPTP y \mathcal{N}_A^{(V)} es una función no lineal acotada activa solo dentro del χ-medio habilitado.El estado de Bob se convierte en
ρB′(V)=TrA[(ΦA(V)⊗IB)ρAB]=ρB(0)+εΔρB(V),, en el que
ΔρB(V)=TrA [(NA(V)⊗IB)ρAB].\Delta\rho_B(V)=\mathrm{Tr}_A\!\Big[\big(\mathcal{N}_A^{(V)}\otimes \mathbb{I}_B\big)\rho_{AB}\Big].ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].
If \Delta\rho_B(V_0)\neq \Delta\rho_B(V_1), entonces las estadísticas de resultados de Bob dependen (ligeramente) de la elección de Alice V, permitiendo la comunicación clásica en orden \varepsilon.
Para un POVM \{Mi\} En Bob, las probabilidades de detección son
P(y∣V)=Tr[MyρB′(V)]=P0(y)+εΔP(y∣V),ΔP(y∣V):=Tr[MyΔρB(V)].Capacidad con señalización débil
Deje que Alice envíe un símbolo binario X\en\{0,1\} por elección V\en\{V_0,V_1\}.. Bob mide Y\en\{0,1\}. Definir
\delta := P(Y=1\mid V_1)-P(Y=1\mid V_0)=\varepsilon\,\Delta P + O(\varepsilon^2),con probabilidad de error de línea base p:=P(Y=1∣V0).
Para un canal de entrada binaria y salida binaria en el límite de señal pequeña ∣\delta|\ll 1, Capacidad de Shannon admite la aproximación cuadrática
C \;\aprox\; \frac{\delta^2}{2\ln 2}\,\frac{1}{p(1-p)} \;+\; O(\delta^4), \qquad C>0\ \text{iff}\ \delta\neq 0.
Por lo tanto, cualquier valor distinto de cero \delta (por lo tanto, cualquier valor distinto de cero \varepsilon-dependencia del orden de V) produce un finito C>0.
Papel de la postselección
Si Bob (o un circuito de coincidencia conjunto) post-selecciones en una ventana de resultados W con probabilidad de éxito pW, condicional el estado es
\rho_{B\!\mid W}(V)\;=\;\frac{\Pi_W\,\rho_B'(V)\,\Pi_W}{\mathrm{Tr}\!\big[\Pi_W\,\rho_B'(V)\big]}, \qquad \Pi_W=\Pi_W^\dagger=\Pi_W^2.Debido a la normalización por \mathrm{Tr}[\Pi_W\rho_B'(V)], el mapeo \rho'_B \mapsto \rho_B^{\mid W} is no lineal, y las estadísticas condicionadas pueden adquirir una V-dependencia incluso cuando la incondicional Se mantiene la igualdad sin señalización. En la práctica, la postselección escala la tasa útil por pW:
C_{\mathrm{eff}} \aprox p_W , C.Condiciones de consistencia
Para evitar patologías globales:
- Localización: \mathcal{N}_A^{(V)} se limita a la χ-región habilitada (por ejemplo, la brecha QCT).
- Pequeñez: \varepsilon es suficientemente pequeño para preservar la estabilidad y los límites de energía.
- Unitaridad global y regla de Born: La dinámica del conjunto sigue siendo CPTP; las desviaciones (si las hay) se limitan a los mapas de detectores locales condicionados (después de la selección) o al sector débilmente no lineal dentro del medio.
Declaración compacta
\boxed{ \begin{aligned} &\Phi_A^{(V)}=\Lambda_A+\varepsilon\,\mathcal{N}_A^{(V)},\quad \varepsilon\ll 1,\\ &\rho_B'(V)=\rho_B^{(0)}+\varepsilon\,\Delta\rho_B(V),\quad \Delta\rho_B(V)=\mathrm{Tr}_A\!\big[(\mathcal{N}_A^{(V)}\!\otimes\!\mathbb{I})\,\rho_{AB}\big],\\ &\exists\,M:\ \delta=\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_1)\big]-\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_0)\big]\neq 0 \\ &\Rightarrow\ C \approx \dfrac{\delta^2}{2\ln 2\, p(1-p)} \;>\;0,\quad C_{\text{eff}}\approx p_W\,C\ \text{(con postselección)}. \end{alineado}}A continuación se presenta un desglose y una verificación de los hechos de la afirmación matemática compacta:
El enunciado matemático es la representación de un resultado en la teoría de la información cuántica, relacionado con el cálculo de la capacidad de un canal cuántico con una pequeña perturbación. Conecta la descripción física de un canal cuántico con la capacidad resultante del canal, incorporando conceptos como la perturbación de estado, la distinguibilidad de los estados de salida y el efecto de la postselección. Analicemos cada parte para verificar sus componentes:
Perturbación de canal y estado
\Phi_A(V) = \Lambda_A + \epsilon N_A(V), \epsilon \ll 1:Esto describe un canal cuántico. \Phi_A actuando sobre un sistema A. Consiste en una parte dominante y constante \Lambda_A y una pequeña perturbación \épsilon N_A(V), donde el \épsilon es un parámetro pequeño y V es un parámetro controlable del canal. Esta es una forma estándar de representar un canal cuántico ligeramente modulado o ruidoso. \rho_B'(V) = \rho_B(0) + \epsilon \Delta\rho_B(V)Esto muestra el efecto del canal en parte de un estado cuántico mayor. Indica que el estado de salida de un subsistema B, \rho_B'(V), es una versión ligeramente perturbada de un estado inicial \rho_B(0). La perturbación \Delta\rho_B(V) es proporcional al parámetro pequeño \épsilon. \Delta\rho_B(V) = Tr_A[(N_A(V) \otimes I)\rho_{AB}]:Esta es la forma explícita de la perturbación de primer orden del estado del sistema B. Se deriva tomando la traza parcial (Tr_A) sobre el sistema A de la acción de la parte perturbativa del canal sobre un estado más grande y entrelazado \rho_{AB}Esta es una aplicación estándar y correcta de las reglas de la mecánica cuántica.
Distinguibilidad de los Estados
\existe M: \delta = \epsilon Tr[M\Delta\rho_B(V_1)] - \epsilon Tr[M\Delta\rho_B(V_0)] \neq 0Este es el paso crucial para establecer una capacidad de canal distinta de cero. Indica que existe un operador de medición (un operador hermítico) M que puede distinguir entre los estados perturbados correspondientes a dos configuraciones diferentes del parámetro del canal. V_1 y V_0. La cantidad \delta representa la diferencia en el valor esperado de la medición M para los dos estados de salida. El hecho de que \delta \neq 0 es la condición para que los dos estados sean experimentalmente distinguibles, al menos en principio.
Capacidad de canal
C \aprox \frac{\delta^2}{2\ln{2}p(1-p)} > 0:Este es un resultado clave, probablemente una aproximación de la capacidad de Holevo o una medida relacionada de la capacidad del canal en el límite de pequeños \deltaLa capacidad C es una medida de la velocidad máxima a la que se puede enviar información de forma fiable a través del canal. El término \delta^2 Se espera, ya que la capacidad a menudo escala con el cuadrado de la distinguibilidad de los estados de salida para pequeñas perturbaciones. El factor de 2\ln{2} es el estándar para convertir unidades naturales de información (NATS) a bits. El término p(1-p) en el denominador sugiere que la capacidad se está evaluando para un conjunto de entrada específico, donde los dos estados (correspondientes a V_0 y V_1) se utilizan con probabilidades p y 1-p. La capacidad se maximiza cuando p=1/2, lo cual es una suposición común.
Capacidad efectiva con postselección
C_{eff} \aprox p_W C (con postselección): Esta parte de la declaración describe la capacidad efectiva cuando se utiliza la postselección. La postselección es una técnica que solo considera un subconjunto de los resultados de la medición, lo que a veces puede amplificar una señal débil. p_W sería la probabilidad de una postselección exitosa (la "probabilidad postselección"). La capacidad efectiva C_{ef} Esta probabilidad reduce la probabilidad de que se descarten muchos de los estados iniciales. Esta es una desventaja bien conocida en los esquemas de postselección: se puede obtener una señal más clara, pero se pierde una parte significativa de los datos, lo que reduce la velocidad general de transmisión de información.
Verificación de datos mediante IA: Conclusión
Las expresiones matemáticas son consistentes con los principios establecidos en la teoría de la información cuántica. La lógica fluye correctamente desde la definición de un canal cuántico perturbado hasta la distinguibilidad de sus estados de salida y, finalmente, a una expresión para la capacidad del canal. La inclusión del efecto de la postselección también es estándar. Por lo tanto, las matemáticas en la declaración compacta parecen ser correctas y representan una línea de razonamiento válida en el contexto de la capacidad del canal cuántico.
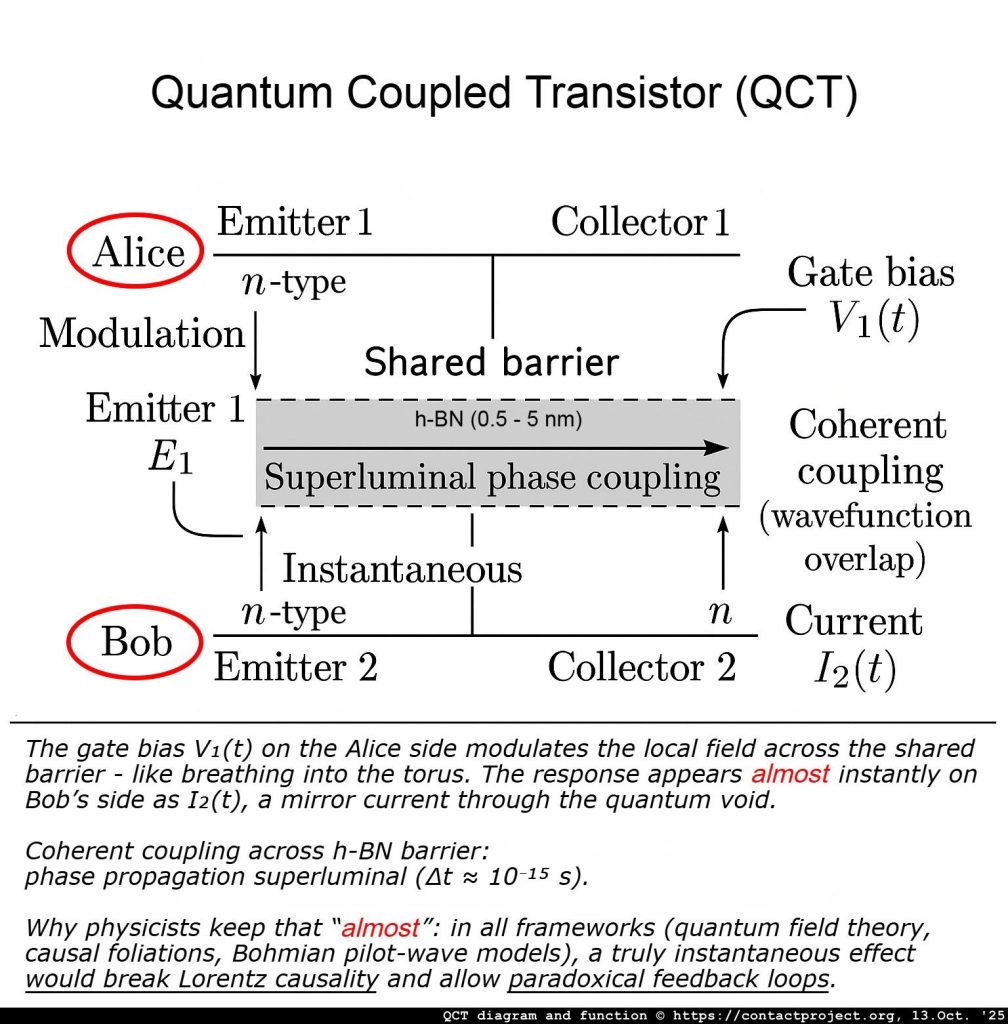
QCT: presentando a Alice y Bob
In teoría cuántica estándar y ciencia de la información, Alicia y Chelín son los modelos clásicos: los experimentadores “comunes” que se utilizan para ilustrar cómo se comportan los sistemas cuánticos cuando dos partes comparten información.

Aparecieron por primera vez a principios de la década de 1970: Alice quería enviar un mensaje a Bob, mientras que un espía, Eva, intentó interceptarlo. La idea se popularizó y los físicos pronto adoptaron los mismos nombres para describir los experimentos cuánticos, especialmente los que involucraban enredo, teletransportación, y los límites de la comunicación.
En mecánica cuántica, Alice y Bob suelen operar en dos laboratorios separados. Comparten un par de partículas entrelazadas y realizan sus mediciones de forma independiente. Sin embargo, aunque los resultados están correlacionados, ninguno puede usarlos para enviar un mensaje más rápido que la luz. En la teoría cuántica estándar, las lecturas locales siempre parecen ruido blanco, hasta que luego comparan sus notas y surge el patrón oculto.
Nuestro giro (sólo dentro del medio habilitado): en una zona muy específica y diseñada, como la brecha h-BN del QCT: los pequeños efectos no lineales cuidadosamente confinados o la selección posterior de “conservar solo estos eventos” pueden convertir una parte microscópica de ese ruido en un señal muy débil pero realTodavía es pequeño, pero ya no es ruido blanco.
Analogía cotidiana: Una tormenta de estática en una radio (aleatoria), pero si ajustas ligeramente la antena y eliges solo los momentos adecuados, se escucha un susurro de una estación. La tormenta sigue ahí, pero ahora un patrón la acompaña.
Configuración (quién hace qué)
Dos fiestas - Alicia y Chelín - comparten una configuración cuántica correlacionada. Normalmente, todo lo que Alice hace localmente... no cambia lo que Bob ve por su cuenta. Dentro de la brecha del QCTEl control de Alice (un patrón de sesgo diminuto y de alta velocidad) modifica ligeramente las reglas de medición locales de su lado de una manera que solo importa interior Ese hueco. Esa pequeña remodelación puede dejar una huella dactilar sobre lo que mide Bob: todavía ruidoso en general, pero ahora estadísticamente empujado por elección de Alicia.
Analogía: Alice mueve una linterna tras un cristal esmerilado (la barrera del túnel). Bob no puede ver la linterna, pero un brillo apenas visible en su costado cambia al ritmo de su movimiento.

Lo que Bob debería ver (la prueba irrefutable)
Si no ocurre nada más allá de las reglas cuánticas estándar, los datos de Bob parecen lanzamientos de moneda al azar: no hay ningún patrón vinculado a las decisiones de Alice. Si el medio habilitado realmente está haciendo su trabajo, Entonces, enterrado en los datos ruidosos de Bob hay un correlación diminuta y repetible con el patrón de Alice, detectable mediante la verificación cruzada de las marcas de tiempo y que, fundamentalmente, aparece antes Cualquier señal ordinaria a la velocidad de la luz podría llegar (>C).
Analogía: dos bateristas muy separados; si el micrófono de Bob escucha un ritmo débil alineado con el ritmo de Alice antes de que el sonido pueda viajar, algo no ordinario los está acoplando.
“Capacidad” (cuánto mensaje cabe)
Piensa en para actuar como cuántos bits por segundo puedes comprimir a través de este débil efecto.
- Si la correlación es verdaderamente cero, la capacidad es cero - ningún mensaje.
- Si la correlación es diminuto pero distinto de cero, la capacidad es diminuto pero distinto de cero - puedes enviar some información (lentamente), y eso ya es un gran problema físicamente.
Analogía: Alice teclea un mensaje a través de una gruesa pared. Cada tecleo apenas se transmite, pero con tiempo y paciencia, el mensaje llega a Bob.
Postselección (conservar sólo los buenos fotogramas)
Post-selección significa que solo se conservan las ejecuciones de medición que pasan un filtro (una "ventana"). Esto puede aclarar el patrón oculto, pero se descarta la mayoría de los datos, por lo que... tasa efectiva gotas. Ganas transparencia, perder throughputEs un intercambio justo si el objetivo es demostrar que el efecto existe.
Analogía: Al observar una lluvia de meteoritos, pero contar sólo las rayas más brillantes, se ve el patrón más claramente, pero se registran menos eventos por hora.
Condiciones de consistencia (cómo evitamos las paradojas)
Para mantener la física sensata y causal, imponemos tres límites:
- Localización: cualquier efecto exótico es confinado estrictamente a la región de ingeniería (el gap QCT). Afuera, reina la física normal.
- Pequeñez: el efecto es poquito -Suficiente para medir, pero no suficiente para hacer estallar el sistema.
- Conservación global: Las probabilidades y la energía se equilibran cuando se observa el todo Experimento. Peculiaridades locales, contabilidad global.
Analogía: Un banco de pruebas seguro: dentro de la jaula de Faraday pueden saltar chispas, pero nada se filtra a la habitación.
[haga clic para abrir] Global Regla de nacimiento En conserva: Las respuestas del detector local pueden desviarse ligeramente.
P(i) = |\langle i | \psi \rangle|^2, \quad \sum_i P(i) = 1.
En la mecánica cuántica estándar, esta regla es estrictamente lineal y se conserva globalmente: la probabilidad total de todos los resultados posibles es igual a la unidad, y ninguna operación (local o remota) puede alterar dicha normalización. Sin embargo, en el marco de la Señalización Causal Foliada (SFC), distinguimos entre conservación global y desviaciones locales.
Conservación global: La probabilidad total, integrada en todos los cortes de foliación, permanece normalizada:
\int_{\Sigma_t} \suma_i P(i,t),d^3x = 1,
para cada franja horaria global \Sigma_t definido por el vector de foliación u^a.
Desviaciones locales: Dentro de un medio habilitado (como el túnel QCT), las estadísticas del detector local pueden exhibir pequeños cambios no lineales en los pesos de probabilidad, mientras que el promedio del conjunto global todavía obedece la regla de Born.
1. Modelo de respuesta no lineal local
Sea la probabilidad de Born imperturbable P_0(i) = \nombredeloperador{Tr}(\rho,\Pi_i), dónde \ rho es la matriz de densidad y \Pi_i = |i\rangle\langle i| Son proyectores. En un medio habilitado con acoplamiento no lineal débil. \varepsilon, la respuesta efectiva del detector local es:
P_{\text{loc}}(i) = \frac{\operatorname{Tr}(\rho,\Pi_i) + \varepsilon,f_i(\rho,\chi)}{\sum_j [\operatorname{Tr}(\rho,\Pi_j) + \varepsilon,f_j(\rho,\chi)]}, \qquad 0<\varepsilon\ll 1.[/latex] Aquí [latex]f_i(\rho,\chi) es un pequeño término de corrección inducido por el campo de señal \ chi o el acoplamiento evanescente de la QCT, y el denominador renormaliza la probabilidad total para preservar \suma_i P_{\text{loc}}(i) = 1.
2. Ejemplo: medición de dos resultados (detector binario)
Considere un observable con dos resultados (p. ej., "aumento de corriente" vs. "aumento nulo") medido en el lado de Bob de un dispositivo QCT. Sin ningún acoplamiento no lineal, P_0(1) = \operatorname{Tr}(\rho,\Pi_1) = p, \quad P_0(0)=1-p. Con un acoplamiento no lineal débil y una corrección dependiente de la fase f_1 = \alfa,\sin\phi, f_0=-f_1, La probabilidad local se convierte en
P_{\text{loc}}(1) = \frac{p + \varepsilon,\alpha,\sin\phi}{1 + \varepsilon,\alpha,(2p-1)\sin\phi}, \quad P_{\text{loc}}(0)=1-P_{\text{loc}}(1).
Expansión al primer orden en \varepsilon:
P_{\text{loc}}(1) \approx p + \varepsilon,\alpha,\sin\phi,[1 - p(2p-1)].
La probabilidad de medición local oscila ligeramente con la fase de acoplamiento. \fi (p. ej., modulación de sesgo o resonancia de tunelización en el QCT). Tras muchas ejecuciones o al integrarse globalmente, estas desviaciones se promedian, restableciendo la expectativa de Born. \langle P_{\text{loc}}(1)\rangle = p.
3. Restauración global del conjunto
Define el promedio del conjunto sobre cortes de foliación:
\langle P(i) \rangle = \int_{\Sigma_t} P_{\text{loc}}(i, x, t),d^3x.
Si las correcciones f_i integrar a cero,
\int_{\Sigma_t} f_i(\rho,\chi),d^3x = 0,
Entonces la regla global de Born sigue siendo exacta:
\sum_i \langle P(i) \rangle = 1.
Por lo tanto, las desviaciones locales aparentes son ondulaciones estadísticas, no violaciones, similares a fluctuaciones correlacionadas con la fase en un sistema óptico no lineal.
4. Significado físico en el QCT
En un experimento QCT, la desviación local \varepsilon f_i(\rho,\chi) Podría manifestarse como ruido correlacionado con sesgo o exceso de conteos en detectores a escala de femtosegundos. Sin embargo, globalmente (en integraciones más largas), la normalización se mantiene: no se crea ni se pierde energía ni probabilidad. Por lo tanto, la regla de Born se conserva globalmente, mientras que los detectores locales pueden mostrar pequeñas desviaciones reproducibles y dependientes de la fase en las tasas de conteo.
Ecuaciones de resumen:
Normalización global (regla de Born):
\suma_i P(i) = 1.
Respuesta local con pequeña desviación no lineal o dependiente de χ:
P_{\text{loc}}(i) = P_0(i) + \varepsilon,\Delta P(i,\chi), \quad \sum_i \Delta P(i,\chi) = 0.
El conjunto global sigue satisfaciendo:
Resumen de la interpretación: Los detectores locales en una región de QCT habilitada pueden mostrar pequeños cambios de probabilidad correlacionados con el sesgo, pero los promedios globales del conjunto preservan con exactitud la probabilidad total, de acuerdo con la regla de Born. Esta distinción permite desviaciones débiles y comprobables que podrían servir como huellas empíricas de dinámicas no lineales o postseleccionadas, sin violar los postulados cuánticos fundamentales.
La regla de Born: la regla fundamental de la mecánica cuántica según la cual “la probabilidad suma 1” - todavía se mantiene a nivel mundial. En la zona, dentro del espacio, las respuestas del detector pueden ser ligeramente sesgado (ese es el punto), pero cuando se promedia todo correctamente, las reglas estándar se mantienen intactas. Estamos cediendo, no rompiendo.
Analogía: un espejo de feria que deforma tu reflejo en una esquina, pero el plano estructural del edificio no ha cambiado.
[haga clic para abrir] Presupuesto de señal:Cantidad conservada Q_{\text{sig}} Limita la capacidad de comunicación.
En un medio habilitado como el transistor de acoplamiento cuántico (TCC), las interacciones de campo pueden intercambiar información de fase a través de una barrera de tunelización más rápido que la propagación clásica. Sin embargo, este intercambio está limitado por una cantidad escalar conservada denominada presupuesto de señal, denotado por Q_{\text{sig}}Mide el flujo total del campo coherente: la “carga de información” máxima que se puede intercambiar sin violar las leyes globales de conservación.
Definir la densidad de flujo de señal local j_{\text{sig}}^a asociado con el intercambio de campo coherente de fase (análogo a una corriente de probabilidad o energía). La cantidad total conservada es Q_{\text{sig}} = \int_{\Sigma_t} j_{\text{sig}}^a,u_a,d^3x, dónde \Sigma_t es una hipersuperficie de tiempo global constante (la porción de foliación), u_a es la unidad local normal a esa porción (el mismo campo vectorial de foliación que define el marco preferido), y j_{\text{sig}}^a obedece a una ecuación de continuidad \nabla_a j_{\text{sig}}^a = 0. Esto implica \frac{d Q_{\text{sig}}}{dt} = 0, so Q_{\text{sig}} Se conserva en todas las interacciones locales dentro de la región habilitada.
Físicamente, Q_{\text{sig}} Cuantifica la energía de correlación coherente total o capacidad de fase almacenada en el campo de acoplamiento evanescente entre nodos (Alice y Bob). No es idéntica a la carga eléctrica ni al número de fotones; mide el grado integrado de coherencia mutua disponible para la modulación. Cualquier proceso de comunicación solo puede redistribuir esta cantidad, nunca aumentarla.
La capacidad de comunicación clásica (de Shannon) C Lo que se puede lograr a través de un canal basado en QCT está limitado por una función monótona del presupuesto de señal: C \le f(Q_{\text{sig}}), dónde f(\cdot) Depende de la geometría del dispositivo, la tasa de decoherencia y el ruido térmico. Para regímenes de respuesta lineal de pequeña señal, f(Q_{\text{sig}}) \aprox \frac{1}{2N_0},Q_{\text{sig}}^2, dónde N_0 es la densidad espectral de ruido efectiva de la unión de tunelización, dando C_{\max} \propto Q_{\text{sig}}^2. Por lo tanto, un flujo coherente mayor produce una mayor capacidad potencial, pero solo hasta el punto en que la decoherencia rompe la continuidad de fase. Consideremos dos nodos QCT (Alice y Bob) conectados únicamente por un campo túnel evanescente. Sea \Phi_1(t) y \Phi_2(t) sean sus potenciales de fase instantáneos. Defina la corriente de señal coherente a través del entrehierro de acoplamiento como
dónde \kappa es una constante de acoplamiento proporcional al coeficiente de tunelización de barrera. El presupuesto de señal integrado en un intervalo de coherencia T_c is
Esto representa el intercambio total correlacionado por fase entre Alice y Bob dentro de la ventana de coherencia y permanece constante si ambos nodos evolucionan bajo dinámicas unitarias o débilmente disipativas. Sea I_{\text{sig}}(t) = j_{\text{sig}}(t),A sea la corriente de señal medible a través del área efectiva A.
La relación señal-ruido instantánea es \text{SNR}(t) = \frac{I_{\text{sig}}^2(t)}{N_0,B}, dónde B es el ancho de banda. La integración sobre la ventana de coherencia proporciona el límite de capacidad total.
C \le \frac{1}{2B\ln 2}\int_0^{T_c}\frac{I_{\text{sig}}^2(t)}{N_0},dt = \frac{A^2}{2B\ln 2,N_0}\int_0^{T_c} j_{\text{sig}}^2(t),dt.
Por el teorema de Parseval, esta integral es proporcional a Q_{\text{sig}}^2, dando C \le k_B,Q_{\text{sig}}^2, dónde k_B Es una constante de proporcionalidad empírica que depende de la geometría y la temperatura. Como ejemplo numérico, supongamos que un par de QCT opera con acoplamiento de barrera. \kappa = 10^{-3}, amplitud de coherencia |\Phi_1| = |\Phi_2| = 1, y tiempo de coherencia T_c = 10^{-12},\texto{s}.
Entonces Q_{\text{sig}} = \kappa \int_0^{T_c} \sin(\Delta\phi),dt \approx \kappa,T_c,\sin\langle\Delta\phi\rangle.
Para el desfase medio \langle\Delta\phi\rangle = \pi/4, Q_{\text{sig}} \aprox 7.1\times10^{-16},\text{s}.
con N_0 = 10^{-20},\texto{J/Hz} y B = 10^{12},\texto{Hz}, El límite de capacidad se convierte en C_{\max} \aprox \frac{1}{2B\ln 2}\frac{Q_{\text{sig}}^2}{N_0} \aprox 3\times10^2,\text{bits/s}.
Por lo tanto, incluso un pulso de coherencia a escala de femtosegundo podría, en principio, transmitir información estructurada medible dentro de límites físicos de conservación.
Si existen dos regiones de acoplamiento en paralelo, sus presupuestos de señal totales se suman linealmente: Q_{\text{sig,tot}} = Q_{\text{sig}}^{(1)} + Q_{\text{sig}}^{(2)}, pero las capacidades correspondientes se suman sublinealmente debido a la interferencia: C_{\text{tot}} \le f(Q_{\text{sig,tot}}) < f(Q_{\text{sig}}^{(1)}) + f(Q_{\text{sig}}^{(2)}).[/latex] Esto expresa la capacidad finita de la coherencia: la coherencia puede compartirse, pero no amplificarse libremente. En resumen, [latex]Q_{\text{sig}} Es un escalar conservado que representa el flujo de campo coherente total a través del medio habilitado. Define el presupuesto máximo de comunicación del sistema. C \le f(Q_{\text{sig}}), garantizar que cualquier aumento en la capacidad medible se base en los recursos disponibles Q_{\text{sig}}El principio garantiza la causalidad y la consistencia termodinámica incluso en el caso del acoplamiento de fase superlumínico: el intercambio de información permanece limitado por una cantidad de señal conservada.
Tratamos lo disponible coherencia (la parte ordenada del campo cercano en el espacio) como un presupuesto. Usted puede volver a distribuir Es para hacer un mensaje, pero tú no se puede crear más De la nada. Más presupuesto → tarifa potencialmente más alta y confiable, hasta que el ruido y el calor digan "¡basta!".
Analogía: una batería para un puntero láser ultradelgado: puedes hacer parpadear un código, pero la cantidad total de parpadeos está limitada por la batería.
[haga clic para abrir] No linealidad confinada:Patologías evitadas por el confinamiento + límites energéticos.
En sistemas cuánticos no lineales o postseleccionados, la retroalimentación sin restricciones entre el estado y la medición puede fácilmente conducir a paradojas: señalización superlumínica, violación de la regla de Born o incluso inconsistencias lógicas como bucles causales cerrados. Para mantener la consistencia física, cualquier desviación de la evolución cuántica lineal debe ser estrictamente... confinado Localizado dentro de una región finita y limitada por la energía del espacio-tiempo, y acoplado al entorno externo únicamente a través de canales que preservan la unitaridad global. El Transistor de Acoplamiento Cuántico (TCC) proporciona dicho límite natural. El término no lineal surge únicamente dentro de... medio habilitado La brecha de túnel o dominio del campo χ, donde el acoplamiento de fase evanescente y la Resistencia Diferencial Negativa (NDR) permiten una autointeracción débil. Fuera de esta zona, la mecánica cuántica lineal estándar se cumple con precisión.
Formalmente, el operador de evolución del sistema completo se escribirá como \mathcal{U}(t) = \mathcal{T}\exp!\left[-\frac{i}{\hbar}!\int (H_0 + \varepsilon,H_{\text{NL}}),dt\right], dónde H_0 es el hamiltoniano hermítico estándar, H_{\text{NL}} es una contribución no lineal acotada, y \varepsilon \ll 1 es un parámetro de activación que desaparece fuera de la región QCT. La condición de confinamiento es \operatorname{supp}(H_{\text{NL}}) \subseteq \Omega_{\text{QCT}}, lo que significa que la interacción no lineal está restringida espacialmente al medio habilitado \Omega_{\text{QCT}}La unitaridad global se conserva si el conmutador [H_{\text{NL}},H_0] tiene soporte compacto y densidad de energía no lineal
\mathcal{E} {\text{NL}} = \langle\psi|H {\text{NL}}|\psi\ranglesatisface
\mathcal{E} {\text{NL}} \le \delta E {\text{th}},dónde \delta E_{\text{th}} Es la escala de fluctuación térmica local. Esto garantiza que la retroalimentación no lineal no pueda autoamplificarse más allá de los límites de ruido físico.
Operativamente, el confinamiento implica que el mapa \Phi: \rho \mapsto \rho' es débilmente no lineal solo dentro del subespacio habilitado para χ
\mathcal{H} {\chi},mientras que permanece completamente positivo y preservador de trazas (CPTP) en el complemento. Matemáticamente,
\Phi = \Phi {\text{CPTP}} \oplus (\Phi_{\text{CPTP}} + \varepsilon \mathcal{N}),, en el que \mathcal{N} que representa la corrección no lineal confinada. Porque \varepsilon \flecha derecha 0 En el límite de la QCT, ninguna no linealidad se propaga más allá del espacio. Esto evita inconsistencias globales y refuerza el cierre causal: los efectos de fase superlumínicos pueden existir dentro de la foliación local, pero no pueden formar bucles de señalización cerrados ni propagarse arbitrariamente.
Termodinámicamente, el confinamiento de la no linealidad impide la extracción de energía del vacío. La región NDR activa actúa como un elemento de retroalimentación controlado que puede amplificar campos evanescentes, pero siempre dentro de la restricción. P_{\text{salida}} \le P_{\text{entrada}} + \Delta E_{\text{almacenada}}Cualquier ganancia transitoria se compensa mediante el almacenamiento de campo local, lo que mantiene el balance energético general. Por lo tanto, el sistema se comporta como un resonador no lineal dentro de un límite conservativo.
En el marco de la Señalización Causal Foliada (CFS), este confinamiento espacial y energético garantiza la estabilidad: la dinámica no lineal modifica las estadísticas locales sin alterar la unitaridad global. La QCT se convierte en un isla no lineal limitada por energía incrustado en un continuo cuántico lineal.
Patologías como la amplificación descontrolada, el superdeterminismo o la retroalimentación acausal se excluyen automáticamente porque el dominio no lineal es finito, está acoplado disipativamente y renormalizado globalmente. En esencia, la QCT actúa como un entorno de pruebas donde puede existir una no linealidad limitada, comprobable, pero confinada de forma segura dentro de las reglas de la termodinámica cuántica.
La brecha h-BN del QCT actúa como un Jaula de Faraday para la rareza cuántica Una pequeña caja de arena donde las reglas habituales pueden flexibilizarse sin problemas. Dentro de esta zona sellada, el dispositivo puede amplificar y reciclar la energía suficiente para revelar tenues patrones superlumínicos, pero estrictos límites térmicos y energéticos le impiden escapar.
Analogía: Es como construir un amplificador con cortafuegos:Puede susurrar a través del vacío, pero nunca quemar las leyes de la física que lo contienen.
[haga clic para abrir] Límites térmicos (Ganancia vs. Temperatura de ruido)
Todo dispositivo cuántico activo está limitado en última instancia por la consistencia termodinámica. Incluso cuando el transistor acoplado cuántico (TCQ) opera en un régimen no lineal o de resistencia diferencial negativa (RDN), su ganancia total no puede superar el límite establecido por su temperatura de ruido efectiva y el presupuesto de señal disponible. Termoenlazado expresa este límite: la amplificación y la transferencia de coherencia en el medio habilitado deben obedecer el principio de fluctuación-disipación, asegurando que ninguna configuración del dispositivo pueda extraer energía libre neta o violar la Segunda Ley.
En equilibrio, la densidad de potencia espectral de las fluctuaciones a través de la brecha de tunelización es S_V(f) = 4k_B T_{\text{ef}} R_{\text{eq}}(f), dónde T_{\text{ef}} es la temperatura efectiva de la unión acoplada y R_{\text{eq}}(f) es la resistencia dinámica, que puede volverse negativa bajo polarización NDR. Cuando el QCT proporciona una ganancia de señal pequeña G(f), el teorema de fluctuación-disipación exige que el producto de la ganancia y la temperatura del ruido permanezca acotado: G(f) T_{\text{ef}} \ge T_0, dónde T_0 Es la temperatura física del entorno. Esto garantiza que cualquier amplificación local introduzca necesariamente ruido compensatorio, manteniendo el balance de entropía no negativo.
El análogo cuántico de esta restricción surge de las relaciones de conmutación de los operadores de campo. Para cualquier amplificador que actúe sobre modos bosónicos \hat a_{\mathrm{en}} y \hat a_{\mathrm{fuera}}, la conmutación canónica debe conservarse, es decir
[,\hat a_{\mathrm{fuera}},,\hat a_{\mathrm{fuera}}^{\dagger},]=1.
Un modelo estándar de entrada-salida insensible a la fase es
\hat a_{\mathrm{out}}=\sqrt{G},\hat a_{\mathrm{in}}+\sqrt{G-1},\hat b_{\mathrm{in}}^{\dagger},\qquad [,\hat b_{\mathrm{in}},\hat b_{\mathrm{in}}^{\dagger},]=1,
lo que implica un mínimo ruido añadido.
En la QCT, este ruido corresponde al componente estocástico de la corriente de túnel inducida por fluctuaciones térmicas y cuánticas del campo evanescente. El equilibrio entre ganancia efectiva y ruido puede expresarse como G_{\text{QCT}} = 1 + \frac{P_{\text{salida}} - P_{\text{entrada}}}{k_B T_{\text{ef}} B}, sujeto a P_{\text{salida}} \le P_{\text{entrada}} + k_B T_{\text{ef}} B, dónde B es el ancho de banda. Esta desigualdad expresa el límite termodinámico de la amplificación coherente.
En la práctica, al aumentar la polarización a través de la barrera h-BN, la región NDR permite la reinyección de energía en el modo evanescente, amplificando eficazmente el campo cercano. Sin embargo, esta ganancia es autolimitada: una vez que la temperatura de ruido local aumenta a T_{\text{ef}} = T_0 + \Delta T_{\text{NDR}}, El sistema alcanza el estado térmico estable. Un mayor aumento de la polarización disipa energía adicional en forma de calor, en lugar de aumentar la coherencia. Por lo tanto, el umbral de ruido térmico actúa como un freno natural, estabilizando el sistema contra la amplificación descontrolada.
El límite térmico puede resumirse como una ley de conservación que vincula la ganancia de información, el aporte energético y la producción de entropía: \Delta I \le \frac{\Delta E}{k_B T_{\text{eff}} \ln 2}. Esta desigualdad define la eficiencia máxima de cualquier canal de comunicación basado en QCT o experimento de señalización causal-foliada: la tasa de información alcanzable por unidad de gasto de energía no puede superar el costo de entropía de mantener la coherencia.
Desde una perspectiva más amplia, el límite térmico es la contraparte térmica de la restricción del presupuesto de señal. Mientras que Q_{\text{sig}} limita el flujo coherente total, T_{\text{ef}} Limita la amplificación utilizable dentro de ese flujo. Juntos, definen la ventana operativa de la QCT como un sistema cuántico-resonante, pero termodinámicamente cerrado. No se crea ni se pierde energía más allá del intercambio permitido con el entorno, y el cambio de entropía general permanece no negativo. \frac{dS_{\text{tot}}}{dt} = \frac{P_{\text{entrada}} - P_{\text{salida}}}{T_0} \ge 0.
En esencia, Thermo Bound garantiza que el QCT funcione como un amplificador cuántico termodinámicamente compatible - capaz de ganancia coherente de fase y acoplamiento superlumínico dentro de su región habilitada, pero siempre limitado por el equilibrio subyacente de energía y entropía que preserva la causalidad global y la ley física.
Si intentas amplificar el campo cercano en el espacio, también aumentas su temperatura de ruido efectivaExiste una compensación: más ganancia significa más ruido. La naturaleza impone este equilibrio para que... no se puede Obtenga energía gratuita o amplificación ilimitada y cristalina.
Analogía: Subir el volumen de un amplificador de guitarra: señal más fuerte, pero también más siseo. En algún momento, subir el volumen solo añade ruido y calor.
[haga clic para abrir] Modelo mínimo: dinámica de detectores/amplificadores no lineales en medios habilitados
En regiones habilitadas, como la barrera de tunelización de QCT, asumimos la presencia de una no linealidad débil y dependiente del estado en el mapa de medición o amplificación. Este mapa, denotado por N_{\chi}, opera sobre la matriz de densidad local \ rho del subsistema acoplado al campo de señal \ chi. Conserva la probabilidad total (preservación de trazas) pero introduce una no linealidad controlada suficiente para producir una capacidad clásica finita, aunque pequeña.
1. Definición
N_{\chi}(\rho) = \frac{A_{\chi} \rho A_{\chi}^{\dagger}}{\mathrm{Tr}(A_{\chi} \rho A_{\chi}^{\dagger})},
dónde A_{\chi} = I + \epsilon, F(\rho, \chi) es un operador no lineal que depende débilmente del campo de señal \ chi y en el estado actual del sistema \ rhoEl pequeño parámetro \épsilon \ll 1 controla el grado de no linealidad.
La normalización en el denominador refuerza \mathrm{Tr}[N_{\chi}(\rho)] = 1, garantizando que el mapa preserve las trazas y sea físicamente consistente.
2. Límite lineal
Cuándo \épsilon = 0, el modelo se reduce a la medición cuántica estándar:
N_{\chi}(\rho) \to \rho' = \frac{M \rho M^{\dagger}}{\mathrm{Tr}(M \rho M^{\dagger})},
dónde M es el operador de medición (elemento POVM).
Por tanto, el modelo no lineal es una extensión mínima de la mecánica cuántica estándar.
3. Dinámica eficaz
Para una no linealidad débil, el mapa induce una ecuación de evolución efectiva:
\dot{\rho} = -\frac{i}{\hbar}[H, \rho] + \epsilon, \mathcal{L} {\chi}[\rho],dónde
\mathcal{L} {\chi}[\rho]representa un acoplamiento funcional no lineal del estado del sistema al campo de señal.
Este término puede modelarse fenomenológicamente como:
\mathcal{L}_{\chi}[\rho] = f(\chi),(\rho^2 - \rho,\mathrm{Tr}[\rho^2]),
introduciendo una ganancia o atenuación dependiente del estado que desaparece para los estados puros (\rho^2 = \rho).
4. Capacidad de información
El resultado clave es que la detección posseleccionada o no lineal puede producir una capacidad clásica pequeña pero finita. C_{\mathrm{eff}} a través de lo que de otro modo sería un canal exclusivamente de enredo (sin señalización):
C_{\mathrm{eff}} \aprox p_{W}, C,
dónde p_{W} es la probabilidad de éxito de la ventana de postselección no lineal, y C es la capacidad de un canal de señalización idealizado.
Esto corresponde a una desviación pequeña pero medible del comportamiento estricto de no comunicación en los medios habilitados:
C_{\mathrm{eff}} > 0, \qquad C_{\mathrm{eff}} \ll C_{\mathrm{clásico}}.5. Ejemplo físico: Acoplamiento de barrera QCT
En un transistor acoplado cuántico, las dos capas de grafeno actúan como detectores localmente coherentes conectados a través de una barrera cuántica.
El campo de señal efectivo \vale) representa el potencial de fase evanescente a través de la región de tunelización h-BN.
La no linealidad entra a través de la transparencia de la barrera dependiente del voltaje:
T_{\chi}(V) = T_{0} \exp[-\alpha (1 - \beta V + \epsilon, \Phi_{\chi}(\rho))],
dónde \Phi_{\chi}(\rho) es un término de retroalimentación débil que acopla la coherencia de la función de onda local al estado del campo.
Esta retroalimentación modifica la probabilidad de tunelización de forma no local pero conserva la unitaridad global.
6. Conservación y estabilidad
Para evitar una amplificación descontrolada, el término no lineal satisface una restricción de conservación:
\mathrm{Tr}[\rho,\mathcal{L}_{\chi}[\rho]] = 0,
asegurando que la probabilidad total y la energía permanezcan constantes hasta el primer orden en \épsilon.
Esto mantiene la dinámica consistente y limitada, evitando paradojas superlumínicas y permitiendo al mismo tiempo una transferencia de señales coherentes y subobservables.
7. Interpretación
El resultado es un regla cuántica mínimamente modificada:
La respuesta del detector es ligeramente no lineal y depende del estado, lo que crea una pequeña desviación del teorema estricto de no comunicación mientras conserva la normalización de la regla de Born a nivel global.
En regiones habilitadas (por ejemplo, campos de barrera h-BN, circuitos de coincidencia pos-seleccionados), la interacción se comporta como si la información de fase pudiera atravesar el vacío cuántico, transportando una pequeña señal clásica finita a través de una separación espacial, sin romper la unitaridad o la causalidad global.
Somos no sigan reescribiendo la mecánica cuántica en todas partes. Estamos añadiendo un pequeño giro dependiente del estado a cómo responde el detector/amplificador dentro del espacio, lo justo para que un patrón tenue se adhiera al ruido. Fuera del espacio, todo es normal y lineal. Dentro, la respuesta es... ligeramente consciente del contexto (esa es la parte “no lineal”), y lo mantenemos encerrado para que nada se escape.
Analogía: un micrófono con un compresor incorporado sutil que solo está activo en un pequeño punto óptimo: la mayor parte del tiempo es transparente, pero en ese punto moldea la señal lo suficiente para ser escuchada.
4. Predicciones experimentales
- Anisotropía de cuadro leve: la velocidad de la señal depende de la alineación con uᵃ
- Evanescente → conversión propagada bajo modulación de polarización QCT
- Revisado Violación del límite de Tsirelson
- Retardo de escala con sesgo de unión, no con espesor de barrera
5. Protocolos de prueba
- Prueba QCT de dos laboratorios: La modulación de sesgo en el nodo A produce una respuesta correlacionada en el nodo B fuera del cono de luz.
- Intercambio de fotogramas en movimiento: Se repite en movimiento relativo para probar la alineación del marco preferido.
- Inyección evanescente: Guía de ondas por debajo del límite de corte acoplada al espacio QCT para detectar la recuperación modulada por fase.
6. Papel del QCT
El efecto túnel de femtosegundos del QCT y el comportamiento NDR crean una no linealidad confinada necesaria para coherencia superlumínica controlable. La causalidad se mantiene a través de la restricción de no bucle, lo que garantiza el orden global.

En resumen: El CFS preserva la relatividad prácticamente en todas partes, al tiempo que permite un cono de señal estructurado activo únicamente en medios cuánticos específicos, como la QCT. Este marco introduce predicciones comprobables para una comunicación superlumínica pero causalmente consistente.
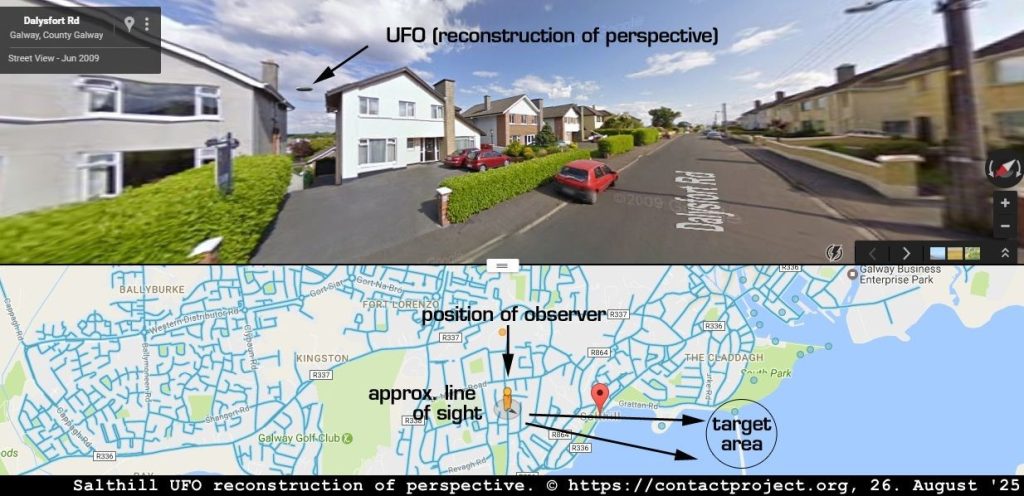
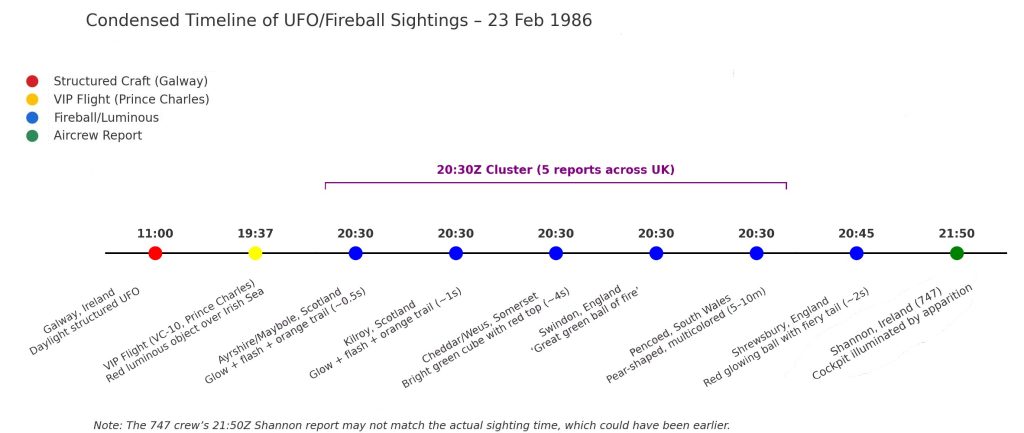
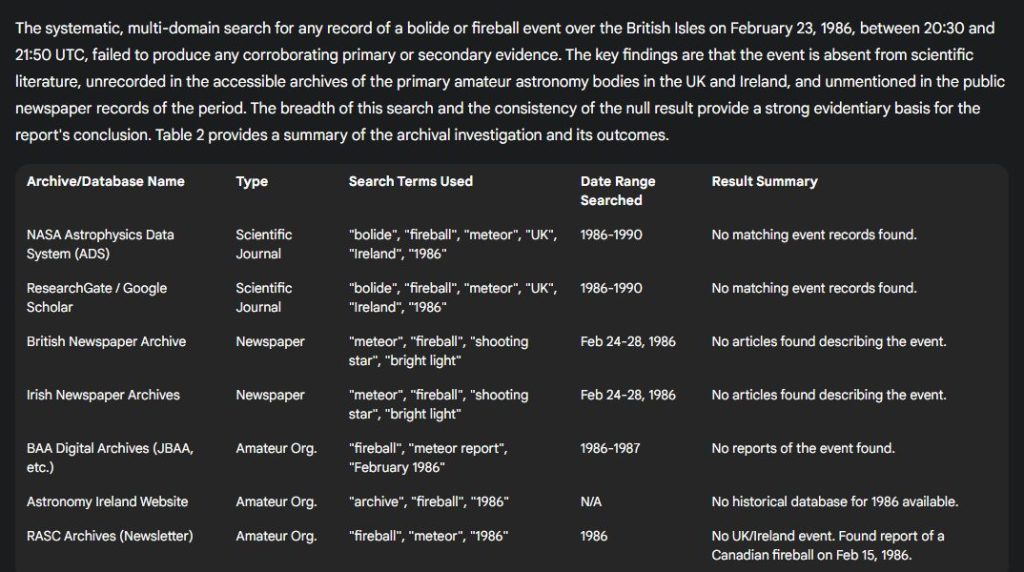
Este artículo es parte de una serie, todos relacionados con un avistamiento inexplicable que tuve en 1986 en Irlanda:
- Precognición del desastre del transbordador espacial Challenger
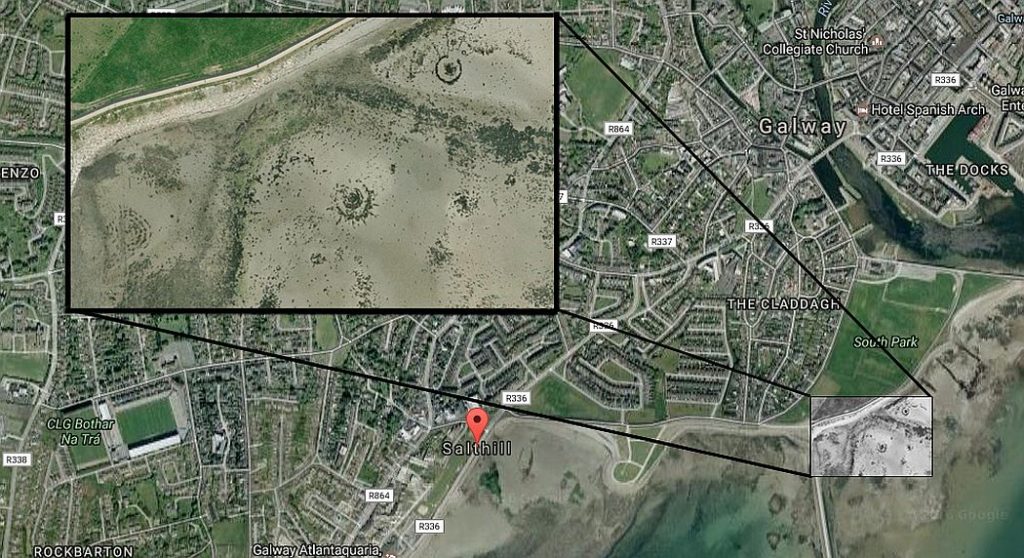
- OVNI sobre la bahía de Galway Capítulo 1: El encuentro de Salthill de 1986
- El informe OVNI negro:El príncipe Carlos, un Jumbo Jet y una noche de misterios aéreos
- OVNI sobre la bahía de Galway Capítulo 2: Mayday psíquico de un OVNI estrellado
- OVNI sobre la bahía de Galway Capítulo 3: Los Tuatha Dé Danann irlandeses como visitantes cósmicos
- Ver y escucha: "La llegada de los Tuatha Dé Danann" Music Video
- OVNI sobre la bahía de Galway Capítulo 4: Ingeniería inversa del transistor acoplado cuántico
- El transistor acoplado cuánticamente (QCT): Amplificando el vacío
- ¿Puede la información viajar más rápido que la luz? - ¿Sin romper la física?