Логика причинно-следственной сигнализации
Теория Причинно-линейная сигнализация (CFS) предполагает, что время содержит скрытые слои, которые обеспечивают ограниченную сверхсветовую когерентность между квантовыми системами. Исследователи вскоре смогут использовать Квантово-связанный транзистор (QCT) – двойное графеновое наноустройство – для непосредственной проверки этих эффектов и определения того, могут ли они возникать, не нарушая известных законов физики.
По сути, CFS задает провокационный вопрос: А что, если определенные виды волн, такие как затухающие или ближние поля, могут обмениваться фазовой информацией быстрее света, но при этом сохранять причинно-следственную связь?
Если это так, то пространство-время может быть не идеально однородным. Оно может содержать тонкую внутреннюю структуру — «слои» времени, где информация немного продвигается вперёд внутри каждого слоя, оставаясь единой в целом.

С этой точки зрения Вселенная разворачивается подобно страницам огромной космической книги: каждая страница переворачивается в идеальном порядке, даже если некоторые страницы переворачиваются чуть быстрее других. КФС предлагает утонченное представление теории относительности, допускающее структурированную сверхсветовую когерентность, сохраняя при этом нетронутой причинно-следственную связь.
Часть II. Причинно-линейная сигнализация (CFS)
- Основные аксиомы
- Кинематика и динамика
- Квантовые правила и законы сохранения
- Экспериментальные предсказания
- Протоколы испытаний
- Роль QCT
1. Основные аксиомы
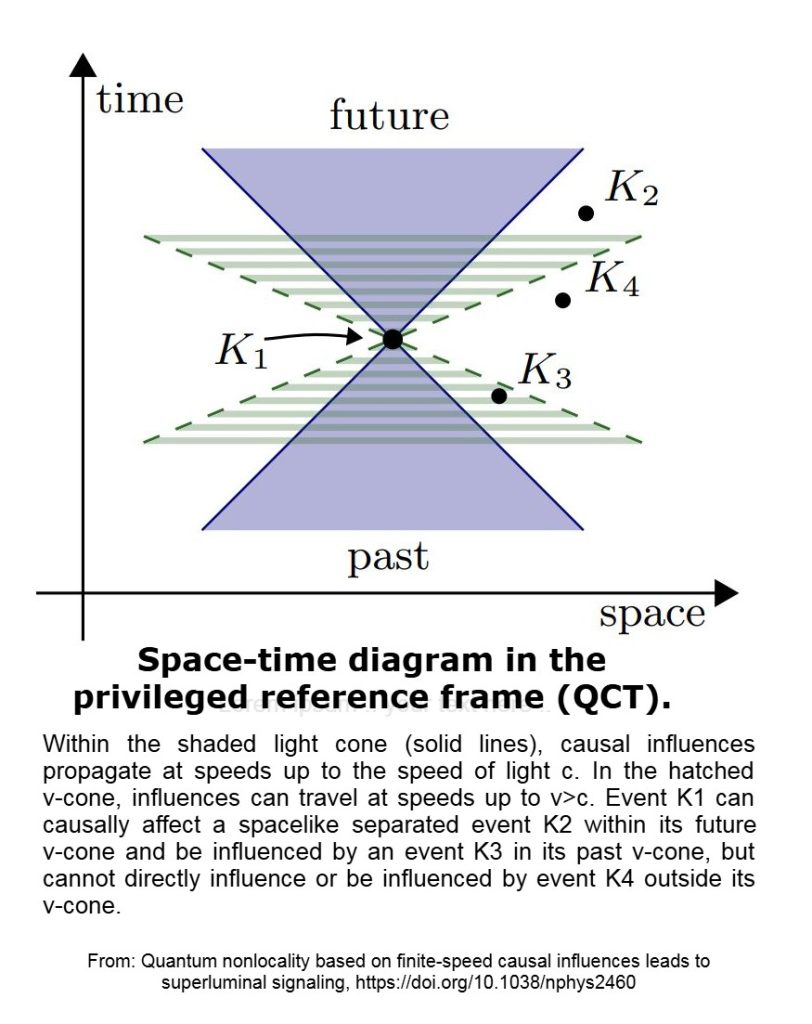
- Глобальная временная фолиация: Пространство-время обладает предпочтительным глобальным нарезом (космическое время, определяемое времениподобным вектором uᵃ). Все сигналы – люминальные и сверхлюминальные – упорядочены этим расслоением.
- Увеличенный сигнальный конус: За световым конусом существует более широкий «сигнальный конус» для определенных сред или полей (χ).
- Защита хронологии: Замкнутые сигнальные контуры динамически запрещены ограничениями разрешимости.
- Операционная местность: Стандартные эксперименты остаются инвариантными относительно Лоренца; отклонения возникают только в разрешенных средах.
2. Кинематика и динамика
- Предпочтительная рамка: Примерно выровнен с рамой покоя CMB.
- Поле сигнала (χ): Слабо связывается с носителями электромагнитного поля, расширяя причинный конус.
- Сверхсветовые характеристики: PDE в разрешенных средах наблюдается распространение за пределами g-светового конуса.
- Ограничение отсутствия цикла: Интегральные условия предотвращают возникновение причинно-следственных петель, уменьшающих время.
3. Квантовые правила и законы сохранения
Мы создали крошечную область (зазор ККТ), где квантовые ближние поля могут быть мягко сформированы так, чтобы едва обнаружимое, сверхсветовое описания проявляется в случайных данных — достаточно малых, чтобы обеспечить безопасность физики, и достаточно четких, чтобы проверить их в лабораторных условиях.

Если приведенное выше краткое утверждение имеет для вас смысл, то вы можете расширить выделенное Квантовые правила ниже, нажав на черные треугольники ▶, можно перейти к БОЛЕЕ подробному обсуждению.
Для широкого круга читателей каждый раздел содержит краткое объяснение (без математических формул), за которым следует аналогия. Хотя большинство людей никогда не слышали о теорема об отсутствии связи (запрещая сверхсветовую связь… с помощью запутывания), она занимает здесь видное место из-за своей фундаментальной важности, а также потому, что контроль релаксация этого правила рассматривается здесь.
[нажмите, чтобы открыть] Смягченная теорема об отсутствии коммуникации: В активированных средах нелинейная/постселективная динамика допускает крошечную классическую емкость > 0.
Претензия (эксплуатационная):
В одном из включенный носитель (например, щель QCT, действующая как ближнее поле с χ-активацией), слабая, локализованная нелинейность or явный пост-отбор может произвести небольшая, но конечная классическая емкость С>0 между пространственно-разделенными сторонами без нарушения глобальной унитарности или правила Борна.
Установка
Позволять ρAB быть двудольным состоянием, разделяемым Алисой и Бобом. В стандартной квантовой механике с локальным Карты CPTP и нет после выбора сокращенное состояние Боба не зависит от выбора Алисы:
ρB′=TrA[(ΦA⊗IB)(ρAB)]=ρB, (без сигнализации)
В одном из включен Регион QCT, модель контролируемой операции Алисы как слабо нелинейный возмущение Карта CPTP:
ΦA(V)(⋅)=ΛA(⋅)+ε\mathcal{N}_A^{(V)}[⋅], 0<ε≪1,[/latex] где [латекс]V является контролем Алисы (например, межслойное смещение), ΛА это CPTP и \mathcal{N}_A^{(V)} — ограниченный нелинейный функционал, действующий только внутри χ-совместимый носитель.Состояние Боба становится
ρB′(V)=TrA[(ΦA(V)⊗IB)ρAB]=ρB(0)+εΔρB(V),
ΔρB(V)=TrA [(NA(V)⊗IB)ρAB].\Delta\rho_B(V)=\mathrm{Tr}_A\!\Big[\big(\mathcal{N}_A^{(V)}\otimes \mathbb{I}_B\big)\rho_{AB}\Big].ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].
If \Delta\rho_B(V_0)\neq \Delta\rho_B(V_1), то статистика результатов Боба зависит (немного) от выбора Алисы V, что позволяет осуществлять классическую коммуникацию по заказу \варепсилон.
Для POVM \{Мой\} на Бобе вероятности обнаружения равны
P(y∣V)=Tr[MyρB′(V)]=P0(y)+εΔP(y∣V),ΔP(y∣V):=Tr[MyΔρB(V)].Емкость со слабой сигнализацией
Пусть Алиса отправит двоичный символ X\в\{0,1\} Выбрав V\в\{V_0,V_1\}.. Боб измеряет Y\в\{0,1\}, определять
\delta := P(Y=1\mid V_1)-P(Y=1\mid V_0)=\varepsilon\,\Delta P + O(\varepsilon^2),с вероятностью базовой ошибки p:=P(Y=1∣V0).
Для канала двоичного входа и двоичного выхода в предел малого сигнала ∣\дельта|\ll 1, Емкость Шеннона допускает квадратичное приближение
C \;\approx\; \frac{\delta^2}{2\ln 2}\,\frac{1}{p(1-p)} \;+\; O(\delta^4), \qquad C>0\ \text{если и только если}\ \delta\neq 0.
Таким образом, любой ненулевой \дельта (следовательно, любой ненулевой \варепсилон-порядковая зависимость от V) дает конечный С>0.
Роль пост-отбора
Если Боб (или совместная схема совпадений) пост-выборы в окне результатов W с вероятностью успеха pW, условный состояние
\rho_{B\!\mid W}(V)\;=\;\frac{\Pi_W\,\rho_B'(V)\,\Pi_W}{\mathrm{Tr}\!\big[\Pi_W\,\rho_B'(V)\big]}, \qquad \Pi_W=\Pi_W^\dagger=\Pi_W^2.Из-за нормализации по \mathrm{Tr}[\Pi_W\rho_B'(V)], отображение \rho'_B \mapsto \rho_B^{\mid W} is нелинейный, и условная статистика может приобрести V-зависимость даже когда безусловный Равенство без сигнализации сохраняется. На практике пост-отбор масштабирует полезную скорость pW:
C_{\mathrm{eff}} \approx p_W , C.Условия согласованности
Чтобы избежать глобальных патологий:
- Локализация: \mathcal{N}_A^{(V)} ограничивается χ-разрешенная область (например, зазор QCT).
- Малость: \варепсилон достаточно мал, чтобы сохранить стабильность и энергетические ограничения.
- Глобальная унитарность и правило Борна: Динамика ансамбля остается CPTP; отклонения (если таковые имеются) ограничиваются условными локальными картами детектора (после отбора) или слабонелинейным сектором внутри среды.
Компактное заявление
\boxed{ \begin{aligned} &\Phi_A^{(V)}=\Lambda_A+\varepsilon\,\mathcal{N}_A^{(V)},\quad \varepsilon\ll 1,\\ &\rho_B'(V)=\rho_B^{(0)}+\varepsilon\,\Delta\rho_B(V),\quad \Delta\rho_B(V)=\mathrm{Tr}_A\!\big[(\mathcal{N}_A^{(V)}\!\otimes\!\mathbb{I})\,\rho_{AB}\big],\\ &\существует\,M:\ \delta=\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_1)\big]-\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_0)\big]\neq 0 \\ &\Rightarrow\ C \approx \dfrac{\delta^2}{2\ln 2\, p(1-p)} \;>\;0,\quad C_{\text{eff}}\approx p_W\,C\ \text{(с пост-селекцией)}. \end{aligned}}Вот анализ и проверка фактов компактного математического утверждения:
Математическое выражение представляет собой представление результата квантовой теории информации, связанного с вычислением пропускной способности квантового канала с малым возмущением. Оно связывает физическое описание квантового канала с результирующей пропускной способностью канала, включая такие концепции, как возмущение состояния, различимость выходных состояний и эффект постселекции. Давайте разберём каждую часть, чтобы проверить её составляющие:
Возмущение канала и состояния
\Ф_А(V) = \Лямбда_А + \эпсилон N_А(V), \эпсилон \ll 1: Это описывает квантовый канал \Phi_A действующий на систему А. Он состоит из доминирующей, постоянной части \Лямбда_А и небольшое возмущение \epsilon N_A(V), Где \эпсилон — малый параметр, а V — некоторый управляемый параметр канала. Это стандартный способ представления слегка модулированного или зашумлённого квантового канала. \rho_B'(V) = \rho_B(0) + \epsilon \Delta\rho_B(V): Это демонстрирует влияние канала на часть более крупного квантового состояния. Это указывает на то, что выходное состояние подсистемы B, \rho_B'(V), представляет собой слегка возмущенную версию начального состояния \rho_B(0). Возмущение \Дельта\ро_Б(В) пропорционален малому параметру \эпсилон. \Дельта\рхо_Б(В) = Тр_А[(Н_А(В) \время I)\рхо_{АБ}]: Это явная форма возмущения первого порядка состояния системы B. Она выводится путем взятия частичного следа (Тр_А) над системой А действия пертурбативной части канала на большее, запутанное состояние \rho_{AB}. Это стандартное и правильное применение правил квантовой механики.
Различимость состояний
\exists M: \delta = \epsilon Tr[M\Delta\rho_B(V_1)] - \epsilon Tr[M\Delta\rho_B(V_0)] \neq 0: Это ключевой шаг для установления ненулевой пропускной способности канала. Он утверждает, что существует оператор измерения (эрмитов оператор) M, который может различать возмущенные состояния, соответствующие двум различным настройкам параметра канала, V_1 и V_0. Количество \дельта представляет собой разницу в ожидаемом значении измерения M для двух выходных состояний. Тот факт, что \дельта \neq 0 является условием того, чтобы два состояния были экспериментально различимы, по крайней мере в принципе.
Пропускная способность канала
C \approx \frac{\delta^2}{2\ln{2}p(1-p)} > 0: Это ключевой результат, вероятно, приближение к пропускной способности Холево или связанная с ней мера пропускной способности канала в пределе малых \дельтаПропускная способность C — это мера максимальной скорости, с которой информация может быть надежно передана по каналу. Термин \дельта^2 Ожидается, поскольку ёмкость часто масштабируется пропорционально квадрату различимости выходных состояний при малых возмущениях. Фактор 2\ln{2} является стандартом для перевода натуральных единиц информации (НАТ) в биты. Термин п(1-п) в знаменателе предполагает, что емкость оценивается для определенного входного ансамбля, где два состояния (соответствующие V_0 и V_1) используются с вероятностями p и 1-p. Ёмкость максимальна, когда р=1/2, что является распространенным предположением.
Эффективная мощность с пост-отбором
C_{eff} \approx p_W C (с пост-отбором): Эта часть утверждения описывает эффективную пропускную способность при использовании пост-отбора. Пост-отбор — это метод, при котором рассматривается только подмножество результатов измерений, что иногда может усилить слабый сигнал. p_W Это вероятность успешного пост-отбора («вероятность пост-отбора»). Эффективная пропускная способность C_{eff} уменьшается на эту вероятность, поскольку многие начальные состояния отбрасываются. Это хорошо известный компромисс в схемах постселекции: вы можете получить более чёткий сигнал, но потеряете значительную часть данных, что снижает общую скорость передачи информации.
Проверка фактов об ИИ: Заключение
Математические выражения согласуются с устоявшимися принципами квантовой теории информации. Логика корректно следует от определения возмущенного квантового канала к различимости его выходных состояний и, наконец, к выражению для пропускной способности канала. Учёт эффекта постселекции также является стандартным. Следовательно, математические выражения в компактной формулировке, по-видимому, корректны и представляют собой корректную цепочку рассуждений в контексте пропускной способности квантового канала.
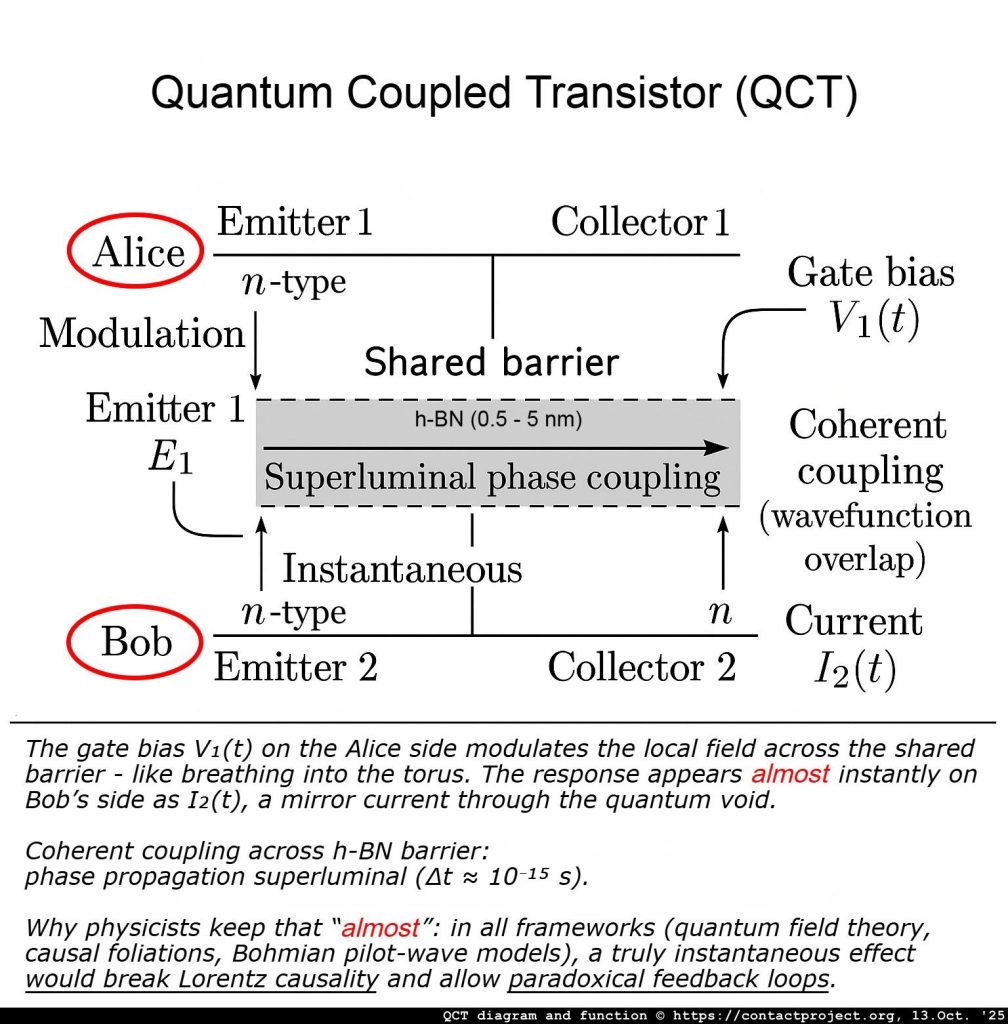
QCT: знакомство с Алисой и Бобом
In стандартная квантовая теория и информационная наука, Alice и боб являются классическими заменителями — экспериментаторами-«обычными людьми», используемыми для иллюстрации поведения квантовых систем, когда две стороны обмениваются информацией.

Впервые они появились в начале 1970-х годов: Алиса хотела отправить сообщение Бобу, в то время как подслушиватель, Ева, попытался перехватить его. Идея прижилась, и физики вскоре стали использовать те же названия для описания квантовых экспериментов, особенно тех, которые связаны с запутанность, телепортацияи пределы общения.
В квантовой механике Алиса и Боб обычно работают в двух отдельных лабораториях. Они совместно используют пару запутанных частиц и проводят измерения независимо друг от друга. Однако, несмотря на корреляцию результатов, ни один из них не может использовать их для передачи данных со сверхсветовой скоростью. В стандартной квантовой теории локальные показания всегда выглядят как белый шум — пока они позже не сравнят показания и не проявится скрытая закономерность.
Наш поворот (только внутри активированной среды): в очень специфической, спроектированной зоне - например, разрыв h-BN ККТ - крошечные, тщательно ограниченные нелинейные эффекты или пост-селекция «сохранить только эти события» могут превратить микроскопическую часть этого шума в очень слабый, но реальный сигнал. Он все еще крошечный, но это уже не белый шум.
Аналогия из повседневной жизни: Шторм помех на радио (случайный), но если слегка наклонить антенну и выбрать только нужные моменты, то можно услышать шёпот станции. Шторм всё ещё там, но теперь на нём есть закономерность.
Настройка (кто что делает)
Две стороны Алиса и боб - совместно использовать коррелированную квантовую установку. Обычно, всё, что Алиса делает локально, не нужна изменить то, что видит Боб, самостоятельно. Внутри разрыва QCT, контроль Алисы (маленький, высокоскоростной шаблон смещения) слегка изменяет локальные правила измерения на ее стороне таким образом, что это имеет значение только внутри Этот зазор. Это крошечное изменение формы может оставить отпечаток пальца на том, что измеряет Боб - в целом все еще шумно, но теперь статистически подтолкнул по выбору Алисы.
Аналогия: Алиса водит фонариком за матовым стеклом (барьером туннеля). Боб не видит фонарик, но едва заметное мерцание на его боку меняется синхронно с её покачиванием.

Что должен увидеть Боб (дымящийся пистолет)
Если не происходит ничего, выходящего за рамки стандартных квантовых правил, данные Боба выглядят как случайные подбрасывания монеты — никакой закономерности, связанной с выбором Алисы. Если включенный носитель действительно выполняет свою работу, затем в шумных данных Боба скрывается крошечная, повторяющаяся корреляция с шаблоном Алисы - который можно обнаружить путем перекрестной проверки временных меток, и, что особенно важно, до любой обычный сигнал со скоростью света может прибыть (>С).
Аналогия: два барабанщика находятся далеко друг от друга; если микрофон Боба слышит слабый удар, совпадающий с ритмом Элис, прежде чем звук успел распространиться, значит, их связывает что-то необычное.
«Вместимость» (объем сообщения)
Подумайте о вместимость сколько бит в секунду вы можете пропустить через этот слабый эффект.
- Если корреляция действительно есть нуль, емкость составляет нуль - нет сообщения.
- Если корреляция есть крошечный, но ненулевой, емкость составляет крошечный, но ненулевой - вы можете отправить некоторых информации (медленно), и это уже имеет большое значение в физическом плане.
Аналогия: Алиса отстукивает сообщение сквозь толстую стену. Звук от каждого удара едва доходит, но со временем и терпением сообщение всё же доходит до Боба.
Пост-отбор (сохранение только хороших кадров)
После выбора означает, что вы сохраняете только те измерения, которые проходят через фильтр («окно»). Это может сделать скрытую закономерность более чёткой, но при этом теряется большая часть данных, поэтому эффективная ставка капли. Вы получаете ясность, свободный пропускная способность. Это честная сделка, если цель — доказать существование эффекта.
Аналогия: наблюдая за метеоритным дождем, но считая только самые яркие полосы, вы видите картину более четко, но регистрируете меньше событий в час.
Условия согласованности (как мы избегаем парадоксов)
Чтобы сохранить разумность и причинность физики, мы устанавливаем три ограничения:
- Локализация: любой экзотический эффект - это ограниченный Строго в пределах инженерной области (зазора ККТ). За пределами царит обычная физика.
- Малость: Эффект крошечный - достаточно для измерения, но недостаточно, чтобы взорвать систему.
- Глобальная охрана природы: Вероятности и энергия уравновешиваются, когда вы смотрите на все Эксперимент. Местные особенности, глобальная бухгалтерия.
Аналогия: безопасный испытательный стенд: внутри клетки Фарадея могут летать искры, но в комнату ничего не просачивается.
[нажмите, чтобы открыть] Глобальный Рожденный Правило Сохранено: Реакции локальных детекторов могут незначительно отличаться.
P(i) = |\langle i | \psi \rangle|^2, \quad \sum_i P(i) = 1.
В стандартной квантовой механике это правило строго линейно и глобально сохраняется: полная вероятность всех возможных исходов равна единице, и никакая операция (локальная или удалённая) не может изменить эту нормировку. Однако в рамках теории причинно-следственной связи (CFS) мы различаем глобальное сохранение и локальные отклонения.
Глобальная охрана природы: Общая вероятность, интегрированная по всем слоям фолиации, остается нормализованной:
\int_{\Sigma_t} \sum_i P(i,t),d^3x = 1,
для каждого глобального временного среза \Сигма_т определяется вектором фолиации у^а.
Местные отклонения: В разрешенной среде (такой как туннельный зазор ККТ) локальная статистика детектора может демонстрировать небольшие нелинейные сдвиги в весовых коэффициентах вероятности, в то время как глобальное среднее по ансамблю по-прежнему подчиняется правилу Борна.
1. Модель локального нелинейного отклика
Пусть невозмущенная вероятность Борна будет P_0(i) = \operatorname{Tr}(\rho,\Pi_i), в котором \ rho это матрица плотности и \Pi_i = |i\rangle\langle i| являются проекторами. В активной среде со слабой нелинейной связью \варепсилон, эффективный локальный отклик детектора равен:
P_{\text{loc}}(i) = \frac{\operatorname{Tr}(\rho,\Pi_i) + \varepsilon,f_i(\rho,\chi)}{\sum_j [\operatorname{Tr}(\rho,\Pi_j) + \varepsilon,f_j(\rho,\chi)]}, \qquad 0<\varepsilon\ll 1.[/latex] Здесь [латекс]f_i(\rho,\chi) небольшой поправочный член, вызванный полем сигнала \ чи или мимолетная связь ККТ, а знаменатель перенормирует общую вероятность сохранения \sum_i P_{\text{loc}}(i) = 1.
2. Пример: измерение с двумя результатами (бинарный детектор)
Рассмотрим наблюдаемую величину с двумя результатами (например, «увеличение тока» и «отсутствие увеличения»), измеренную на стороне Боба в устройстве квантовой компьютерной томографии. Без какой-либо нелинейной связи P_0(1) = \operatorname{Tr}(\rho,\Pi_1) = p, \quad P_0(0)=1-p. Со слабой нелинейной связью и фазозависимой коррекцией f_1 = \альфа,\син\фи, f_0=-f_1, локальная вероятность становится
P_{\text{loc}}(1) = \frac{p + \varepsilon,\alpha,\sin\phi}{1 + \varepsilon,\alpha,(2p-1)\sin\phi}, \quad P_{\text{loc}}(0)=1-P_{\text{loc}}(1).
Расширение до первого порядка в \варепсилон:
P_{\text{loc}}(1) \approx p + \varepsilon,\alpha,\sin\phi,[1 - p(2p-1)].
Вероятность локального измерения слегка колеблется в зависимости от фазы связи \ Phi (например, модуляция смещения или туннельный резонанс в квантовой теории квантовых вычислений). При многократном прогоне или при глобальном интегрировании эти отклонения усредняются, восстанавливая ожидаемое значение Борна. \langle P_{\text{loc}}(1)\rangle = p.
3. Ансамблевая (глобальная) реставрация
Определим среднее значение ансамбля по слоям фолиации:
\langle P(i) \rangle = \int_{\Sigma_t} P_{\text{loc}}(i, x, t),d^3x.
Если исправления ебать интегрировать до нуля,
\int_{\Sigma_t} f_i(\rho,\chi),d^3x = 0,
то глобальное правило Борна остается точным:
\sum_i \langle P(i) \rangle = 1.
Таким образом, кажущиеся локальные отклонения представляют собой статистические колебания, а не нарушения — сродни фазово-коррелированным флуктуациям в нелинейной оптической системе.
4. Физический смысл в квантовой теории квантовой механики
В эксперименте QCT локальное отклонение \varepsilon f_i(\rho,\chi) может проявляться в виде шума, коррелированного со смещением, или избыточных отсчётов в фемтосекундных детекторах. Однако в глобальном масштабе (при более длительной интеграции) нормализация сохраняется — энергия или вероятность не создаются и не теряются. Следовательно, правило Борна сохраняется в глобальном масштабе, в то время как локальные детекторы могут демонстрировать небольшие, воспроизводимые, зависящие от фазы отклонения в скорости счёта.
Суммарные уравнения:
Глобальная нормализация (правило Борна):
\sum_i P(i) = 1.
Локальный отклик с небольшим нелинейным или χ-зависимым отклонением:
P_{\text{loc}}(i) = P_0(i) + \varepsilon,\Delta P(i,\chi), \quad \sum_i \Delta P(i,\chi) = 0.
Глобальный ансамбль по-прежнему удовлетворяет:
Краткое изложение интерпретации: Локальные детекторы в области квантовой квантовой теории (ККТ) могут демонстрировать небольшие, коррелированные со смещением сдвиги вероятности, но глобальные ансамблевые усреднения точно сохраняют полную вероятность, в соответствии с правилом Борна. Это различие допускает слабые, проверяемые отклонения, которые могут служить эмпирическими отпечатками нелинейной или постселективной динамики, не нарушая при этом основные квантовые постулаты.
Правило Борна — основное правило квантовой механики «вероятность прибавляется к 1». - все еще действует в глобальном масштабе. в местном масштабе, внутри зазора, ответы детектора могут быть слегка перекошено (в этом-то и суть), но если всё усреднить, то стандартные правила останутся неизменными. Мы сгибаем, а не ломаем.
Аналогия: кривое зеркало, искажающее ваше отражение в углу, но структурная схема здания не изменилась.
[нажмите, чтобы открыть] Бюджет сигнала: Сохраняемое количество Q_{\text{sig}} Ограничения пропускной способности коммуникаций.
В среде с активным взаимодействием, такой как квантово-связанный транзистор (КТТ), полевые взаимодействия могут передавать фазовую информацию через туннельный барьер быстрее, чем при классическом распространении. Однако этот обмен ограничен сохраняющейся скалярной величиной, называемой бюджет сигнала, обозначается Q_{\text{sig}}. Он измеряет полный поток когерентного поля — максимальный «информационный заряд», которым можно обмениваться, не нарушая глобальных законов сохранения.
Определить локальную плотность потока сигнала j_{\text{sig}}^a Связанный с фазово-когерентным обменом полями (аналогично току вероятности или энергии). Общая сохраняющаяся величина равна Q_{\text{sig}} = \int_{\Sigma_t} j_{\text{sig}}^a,u_a,d^3x, в котором \Сигма_т является гиперповерхностью постоянного глобального времени (слой фолиации), у_а является локальной единицей, нормалью к этому срезу (то же самое векторное поле фолиации, определяющее предпочтительную систему координат), и j_{\text{sig}}^a подчиняется уравнению непрерывности \nabla_a j_{\text{sig}}^a = 0. Из этого следует \frac{d Q_{\text{sig}}}{dt} = 0, so Q_{\text{sig}} сохраняется при всех локальных взаимодействиях в пределах разрешенной области.
Физически, Q_{\text{sig}} Количественно определяет общую когерентную корреляционную энергию или фазовую ёмкость, хранящуюся в затухающем поле связи между узлами (Алисой и Бобом). Она не тождественна электрическому заряду или числу фотонов, а скорее измеряет интегральную степень взаимной когерентности, доступную для модуляции. Любой процесс коммуникации может лишь перераспределить эту величину, но не увеличить её.
Классическая (Шенноновская) коммуникационная способность C достижимый через канал на основе QCT, ограничен монотонной функцией бюджета сигнала: C \le f(Q_{\text{sig}}), в котором f(\cdot) зависит от геометрии устройства, скорости декогеренции и теплового шума. Для режимов с малым сигналом и линейным откликом f(Q_{\text{sig}}) \approx \frac{1}{2N_0},Q_{\text{sig}}^2, в котором Н_0 эффективная спектральная плотность шума туннельного перехода, дающая C_{\max} \propto Q_{\text{sig}}^2. Таким образом, больший когерентный поток обеспечивает более высокую потенциальную ёмкость, но только до точки, где декогеренция нарушает непрерывность фазы. Рассмотрим два узла ККТ (Алису и Боба), соединённых только эванесцентным туннельным полем. Пусть \Фи_1(т) и \Фи_2(т) Пусть их мгновенные фазовые потенциалы. Определим ток когерентного сигнала через зазор связи как
в котором \каппа — константа связи, пропорциональная коэффициенту туннелирования барьера. Интегральный бюджет сигнала на одном интервале когерентности Т_с is
Это представляет собой полный фазово-коррелированный обмен между Алисой и Бобом в пределах окна когерентности и остаётся постоянным, если оба узла развиваются в условиях унитарной или слабодиссипативной динамики. Пусть I_{\text{sig}}(t) = j_{\text{sig}}(t),A быть измеряемым током сигнала через эффективную площадь A.
Мгновенное отношение сигнал/шум равно \text{SNR}(t) = \frac{I_{\text{sig}}^2(t)}{N_0,B}, в котором B Это пропускная способность. Интеграция по окну когерентности даёт общую ограниченную пропускную способность.
C \le \frac{1}{2B\ln 2}\int_0^{T_c}\frac{I_{\text{sig}}^2(t)}{N_0},dt = \frac{A^2}{2B\ln 2,N_0}\int_0^{T_c} j_{\text{sig}}^2(t),dt.
По теореме Парсеваля этот интеграл пропорционален Q_{\text{sig}}^2, предоставление C \le k_B,Q_{\text{sig}}^2, в котором к_Б — эмпирический коэффициент пропорциональности, зависящий от геометрии и температуры. Для численного примера предположим, что пара квантовых термодинамических резонансов работает с барьерной связью. \каппа = 10^{-3}, амплитуда когерентности |\Фи_1| = |\Фи_2| = 1, и время когерентности T_c = 10^{-12},\text{с}.
Затем Q_{\text{sig}} = \kappa \int_0^{T_c} \sin(\Delta\phi),dt \approx \kappa,T_c,\sin\langle\Delta\phi\rangle.
Для средней задержки фазы \langle\Delta\phi\rangle = \pi/4, Q_{\text{sig}} \approx 7.1\times10^{-16},\text{s}.
Для пользователя
N_0 = 10^{-20},\text{Дж/Гц} и B = 10^{12},\text{Гц}, ограничение емкости становится C_{\max} \approx \frac{1}{2B\ln 2}\frac{Q_{\text{sig}}^2}{N_0} \approx 3\times10^2,\text{бит/с}.
Таким образом, даже фемтосекундный когерентный импульс может, в принципе, передавать измеримую структурированную информацию в пределах физических ограничений сохранения.
Если две области связи существуют параллельно, их общие сигнальные бюджеты складываются линейно: Q_{\text{sig,tot}} = Q_{\text{sig}}^{(1)} + Q_{\text{sig}}^{(2)}, но соответствующие емкости добавляются сублинейно из-за интерференции: C_{\text{tot}} \le f(Q_{\text{sig,tot}}) < f(Q_{\text{sig}}^{(1)}) + f(Q_{\text{sig}}^{(2)}).[/latex] Это выражает ограниченность когерентности: когерентность может быть передана, но не может быть произвольно усилена. Подводя итог, [latex]Q_{\text{sig}} — сохраняющийся скаляр, представляющий собой полный поток когерентного поля через активную среду. Он определяет максимальный коммуникационный бюджет системы, C \le f(Q_{\text{sig}}), гарантируя, что любое увеличение измеримой мощности будет исходить из имеющихся Q_{\text{sig}}. Этот принцип гарантирует причинность и термодинамическую согласованность даже при сверхсветовой фазовой связи: обмен информацией остаётся ограниченным сохраняющейся величиной сигнала.
Мы относимся к имеющимся согласованность (упорядоченная часть ближнего поля в зазоре) как бюджет. Вы можете Перераспределение чтобы сделать сообщение, но вы не могу создать больше С нуля. Больше бюджета → потенциально более высокая надёжная ставка, пока шум и жара не скажут «стоп».
Аналогия: батарейка для сверхтонкой лазерной указки: вы можете моргнуть кодом, но общее количество миганий ограничено батареей.
[нажмите, чтобы открыть] Ограниченная нелинейность: Патологии, которых можно избежать с помощью ограничения свободы и энергетических ограничений.
В нелинейных или постселективных квантовых системах неограниченная обратная связь между состоянием и измерением может легко привести к парадоксам: сверхсветовой передаче сигналов, нарушению правила Борна или даже логическим противоречиям, таким как замкнутые причинно-следственные связи. Для сохранения физической согласованности любое отклонение от линейной квантовой эволюции должно быть строго ограниченный - локализованы в конечной, энергетически ограниченной области пространства-времени и связаны с внешней средой только через каналы, сохраняющие глобальную унитарность. Квантовый транзистор (КТ) обеспечивает такую естественную границу. Нелинейный член возникает только внутри включенный носитель – туннельная щель, или область χ-поля, – где затухающая фазовая связь и отрицательное дифференциальное сопротивление (ОДС) допускают слабое самовзаимодействие. Вне этой зоны стандартная линейная квантовая механика выполняется точно.
Формально пусть полный оператор эволюции системы записывается как \mathcal{U}(t) = \mathcal{T}\exp!\left[-\frac{i}{\hbar}!\int (H_0 + \varepsilon,H_{\text{NL}}),dt\right], в котором H_0 — стандартный эрмитов гамильтониан, H_{\text{NL}} является ограниченным нелинейным вкладом, и \varepsilon \ll 1 – параметр активации, который обращается в нуль вне области квантовой квантовой теории. Условие ограничения: \operatorname{supp}(H_{\text{NL}}) \subseteq \Omega_{\text{QCT}}, что означает, что нелинейное взаимодействие пространственно ограничено разрешенной средой \Omega_{\text{QCT}}Глобальная унитарность сохраняется, если коммутатор [H_{\text{NL}},H_0] имеет компактный носитель и нелинейную плотность энергии
\mathcal{E} {\text{NL}} = \langle\psi|H {\text{NL}}|\psi\rangleудовлетворяет
\mathcal{E} {\text{NL}} \le \delta E {\text{th}},в котором \delta E_{\text{th}} — это локальный масштаб тепловых флуктуаций. Это гарантирует, что нелинейная обратная связь не сможет усилиться сверх физических шумовых пределов.
С точки зрения эксплуатации, ограничение свободы подразумевает, что карта \Phi: \rho \mapsto \rho' слабо нелинейна только в подпространстве с χ-разрешением
\mathcal{H} {\chi},при этом он остаётся полностью положительным и сохраняющим след (CPTP) на дополнительном. Математически,
\Phi = \Phi {\text{CPTP}} \oplus (\Phi_{\text{CPTP}} + \varepsilon \mathcal{N}),\mathcal{N} представляющая собой ограниченную нелинейную коррекцию. Поскольку \varepsilon \rightarrow 0 На границе квантовой квантовой теории нелинейность не распространяется за пределы зазора. Это предотвращает глобальные противоречия и обеспечивает причинно-следственную замкнутость: сверхсветовые фазовые эффекты могут существовать внутри локального фолиационного пространства, но не могут образовывать замкнутые сигнальные петли или распространяться произвольно.
С термодинамической точки зрения, ограничение нелинейности гарантирует невозможность извлечения энергии из вакуума. Активная область ОДР действует как управляемый элемент обратной связи, способный усиливать эванесцентные поля, но всегда в рамках ограничений. P_{\text{out}} \le P_{\text{in}} + \Delta E_{\text{stored}}Любое переходное усиление компенсируется локальным накоплением поля, поддерживая общий энергетический баланс. Таким образом, система ведёт себя как нелинейный резонатор, заключённый в консервативную границу.
В рамках теории причинно-следственной фолиированной сигнализации (CFS) это пространственное и энергетическое ограничение гарантирует устойчивость: нелинейная динамика изменяет локальную статистику, не нарушая глобальной унитарности. ККТ становится энергетически ограниченный нелинейный остров встроенный в линейный квантовый континуум.
Такие патологии, как неконтролируемое усиление, супердетерминизм или акаузальная обратная связь, автоматически исключаются, поскольку нелинейная область конечна, диссипативно связана и глобально перенормирована. По сути, ККТ действует как песочница, где может существовать ограниченная нелинейность, проверяемая, но безопасно изолированная в рамках правил квантовой термодинамики.
Разрыв h-BN в QCT действует как Клетка Фарадея для квантовых странностей – крошечная песочница, где обычные правила могут безопасно изменяться, не нарушаясь. Внутри этой изолированной зоны устройство может усиливать и перерабатывать энергию ровно настолько, чтобы обнаруживать слабые сверхсветовые узоры, но строгие тепловые и энергетические ограничения не позволяют ему выйти из-под контроля.
Аналогия: Это похоже на строительство усилитель с брандмауэром: он может шептать сквозь пустоту, но никогда не прожигает законы физики, которые его сдерживают.
[нажмите, чтобы открыть] Thermo Bounds (Усиление в зависимости от шумовой температуры)
Каждое активное квантовое устройство в конечном итоге ограничено термодинамической согласованностью. Даже когда квантово-связанный транзистор (КТТ) работает в нелинейном режиме или режиме отрицательного дифференциального сопротивления (ОДС), его общий коэффициент усиления не может превышать предел, определяемый его эффективной шумовой температурой и доступным сигнальным бюджетом. Термо-связанный выражает этот предел: усиление и передача когерентности в активной среде должны подчиняться принципу флуктуации-рассеивания, гарантируя, что никакая конфигурация устройства не сможет извлечь чистую свободную энергию или нарушить Второй закон.
В состоянии равновесия спектральная плотность мощности флуктуаций в туннельном зазоре равна S_V(f) = 4k_B T_{\text{eff}} R_{\text{eq}}(f), в котором T_{\text{эфф}} эффективная температура связанного перехода и R_{\text{eq}}(f) Это динамическое сопротивление, которое может стать отрицательным при смещении NDR. Когда QCT обеспечивает усиление слабого сигнала, Г(ф), теорема о флуктуации-диссипации требует, чтобы произведение коэффициента усиления и шумовой температуры оставалось ограниченным: G(f) T_{\text{eff}} \ge T_0, в котором T_0 — это физическая температура окружающей среды. Это гарантирует, что любое локальное усиление обязательно вносит компенсирующий шум, поддерживая баланс энтропии неотрицательным.
Квантовый аналог этого ограничения возникает из коммутационных соотношений операторов поля. Для любого усилителя, действующего на бозонные моды, \что_{\mathrm{в}} и \hat a_{\mathrm{out}}, каноническая коммутация должна быть сохранена, т.е.
[,\hat a_{\mathrm{out}},,\hat a_{\mathrm{out}}^{\dagger},]=1.
Стандартная фазонечувствительная модель ввода-вывода:
\hat a_{\mathrm{out}}=\sqrt{G},\hat a_{\mathrm{in}}+\sqrt{G-1},\hat b_{\mathrm{in}}^{\dagger},\qquad [,\hat b_{\mathrm{in}},\hat b_{\mathrm{in}}^{\dagger},]=1,
что подразумевает минимальный дополнительный шум.
В квантовой теории квантовых токов этот шум соответствует стохастической составляющей туннельного тока, вызванной тепловыми и квантовыми флуктуациями затухающего поля. Эффективный компромисс между усилением и шумом можно записать как G_{\text{QCT}} = 1 + \frac{P_{\text{out}} - P_{\text{in}}}{k_B T_{\text{eff}} B}, при условии P_{\text{out}} \le P_{\text{in}} + k_B T_{\text{eff}} B, в котором B — это полоса пропускания. Это неравенство выражает термодинамический предел когерентного усиления.
На практике, при увеличении смещения через барьер h-BN, область NDR обеспечивает обратную инжекцию энергии в затухающую моду, эффективно усиливая ближнее поле. Однако это усиление самоограничено: как только локальная шумовая температура достигает T_{\text{eff}} = T_0 + \Delta T_{\text{NDR}}, Система достигает теплового стационарного состояния. Дальнейшее увеличение смещения рассеивает дополнительную энергию в виде тепла, а не увеличивает когерентность. Таким образом, тепловой шум действует как естественный тормоз, стабилизируя систему, предотвращая неконтролируемое усиление.
Таким образом, термограницу можно свести к закону сохранения, связывающему прирост информации, энергетическую составляющую и производство энтропии: \Дельта I \le \frac{\Дельта E}{k_B T_{\text{eff}} \ln 2}. Это неравенство определяет конечную эффективность любого канала связи на основе квантовой компьютерной томографии или эксперимента по причинно-следственной передаче сигналов: скорость передачи информации, достижимая на единицу затрат энергии, не может превышать энтропийных затрат на поддержание когерентности.
В более широком смысле, термограница является тепловым аналогом ограничения бюджета сигнала. Q_{\text{sig}} ограничивает полный когерентный поток, T_{\text{эфф}} ограничивает применимое усиление в пределах этого потока. Вместе они определяют рабочее окно квантово-резонансной, но термодинамически замкнутой системы. Энергия не создаётся и не теряется за пределами допустимого обмена с окружающей средой, а общее изменение энтропии остаётся неотрицательным: \frac{dS_{\text{tot}}}{dt} = \frac{P_{\text{in}} - P_{\text{out}}}{T_0} \ge 0.
По сути, Thermo Bound обеспечивает работу QCT как термодинамически совместимый квантовый усилитель - способен к фазово-когерентному усилению и сверхсветовой связи в пределах своей разрешенной области, но всегда ограничен базовым балансом энергии и энтропии, который сохраняет глобальную причинность и физические законы.
Если вы попытаетесь усилить ближнее поле в зазоре, вы также повысите его эффективная шумовая температура. Есть компромисс: больше усиления — больше шума. Природа обеспечивает этот баланс, чтобы вы не может получите бесплатную энергию или неограниченное, кристально чистое усиление.
Аналогия: Увеличиваем громкость гитарного усилителя: сигнал громче, но и шипение сильнее. В какой-то момент дополнительная громкость просто добавляет шума и тепла.
[нажмите, чтобы открыть] Минимальная модель: динамика нелинейного детектора/усилителя в активных средах
В разрешенных областях, таких как туннельный барьер квантовой теории квантовых токов (КТ), мы предполагаем наличие слабой, зависящей от состояния, нелинейности в карте измерений или усиления. Эта карта, обозначенная как Н_{\чи}, действует на локальную матрицу плотности \ rho подсистемы, связанной с полем сигнала \ чи. Он сохраняет полную вероятность (сохраняет след), но вводит контролируемую нелинейность, достаточную для получения конечной, хотя и крошечной, классической емкости.
1. Определение
N_{\chi}(\rho) = \frac{A_{\chi} \rho A_{\chi}^{\dagger}}{\mathrm{Tr}(A_{\chi} \rho A_{\chi}^{\dagger})},
в котором A_{\хи} = I + \эпсилон, F(\ро, \хи) — нелинейный оператор, слабо зависящий от поля сигнала \ чи и о текущем состоянии системы \ rho. Малый параметр \эпсилон \ll 1 контролирует степень нелинейности.
Нормализация в знаменателе обеспечивает \mathrm{Tr}[N_{\chi}(\rho)] = 1, гарантируя, что карта сохраняет следы и является физически последовательной.
2. Линейный предел
После появления \эпсилон = 0, модель сводится к стандартному квантовому измерению:
N_{\chi}(\rho) \to \rho' = \frac{M \rho M^{\dagger}}{\mathrm{Tr}(M \rho M^{\dagger})},
в котором M — оператор измерения (элемент POVM).
Таким образом, нелинейная модель представляет собой минимальное расширение стандартной квантовой механики.
3. Эффективная динамика
При слабой нелинейности карта индуцирует эффективное уравнение эволюции:
\dot{\rho} = -\frac{i}{\hbar}[H, \rho] + \epsilon, \mathcal{L} {\chi}[\rho],в котором
\mathcal{L} {\chi}[\rho]представляет собой нелинейную функциональную связь состояния системы с полем сигнала.
Этот термин можно феноменологически смоделировать следующим образом:
\mathcal{L}_{\chi}[\rho] = f(\chi),(\rho^2 - \rho,\mathrm{Tr}[\rho^2]),
введение зависящего от состояния усиления или затухания, которое исчезает для чистых состояний (\rho^2 = \rho).
4. Информационная емкость
Ключевым результатом является то, что постселективное или нелинейное обнаружение может дать небольшую, но конечную классическую емкость. C_{\mathrm{eff}} по каналу, который в противном случае был бы только запутанным (без сигнализации):
C_{\mathrm{eff}} \approx p_{W}, C,
в котором п_{В} вероятность успеха нелинейного окна пост-отбора, и C — это пропускная способность идеализированного канала сигнализации.
Это соответствует небольшому, но измеримому отклонению от строгого поведения отсутствия коммуникации в разрешенных медиа:
C_{\mathrm{eff}} > 0, \qquad C_{\mathrm{eff}} \ll C_{\mathrm{classical}}.5. Физический пример: QCT-барьерная связь
В квантово-связанном транзисторе два слоя графена действуют как локально когерентные детекторы, соединенные квантовым барьером.
Эффективное сигнальное поле \хи(т) представляет собой потенциал затухающей фазы в области туннелирования h-BN.
Нелинейность возникает из-за зависящей от напряжения прозрачности барьера:
T_{\chi}(V) = T_{0} \exp[-\alpha (1 - \beta V + \epsilon, \Phi_{\chi}(\rho))],
в котором \Фи_{\хи}(\ро) — слабый член обратной связи, связывающий локальную когерентность волновой функции с состоянием поля.
Такая обратная связь нелокально изменяет вероятность туннелирования, но сохраняет глобальную унитарность.
6. Сохранение и устойчивость
Чтобы предотвратить неконтролируемое усиление, нелинейный член удовлетворяет ограничению сохранения:
\mathrm{Tr}[\rho,\mathcal{L}_{\chi}[\rho]] = 0,
гарантируя, что общая вероятность и энергия остаются постоянными в первом порядке \эпсилон.
Это сохраняет динамику самосогласованной и ограниченной, избегая сверхсветовых парадоксов и допуская при этом субнаблюдаемую, когерентную передачу сигнала.
7. интерпретация
Результатом является минимально модифицированное квантовое правило:
Реакция детектора слегка нелинейна и зависит от состояния, что создает небольшое отклонение от строгой теоремы об отсутствии связи, сохраняя при этом нормализацию по правилу Борна в глобальном масштабе.
В разрешенных областях (например, барьерные поля h-BN, схемы совпадений после выбора) взаимодействие ведет себя так, как будто фазовая информация может туннелировать через квантовую пустоту, перенося крошечный, конечный классический сигнал через пространственное разделение, не нарушая унитарности или глобальной причинности.
Мы Переписываем квантовую механику повсюду. Мы добавляем крошечный, зависящий от состояния поворот как реагирует детектор/усилитель внутри зазора – ровно настолько, чтобы на шуме присутствовала едва заметная закономерность. Вне зазора всё обычно и линейно. Внутри же отклик немного учитывающий контекст (это «нелинейная» часть), и мы сохраняем его ограниченный так что ничего не убежит.
Аналогия: микрофон с едва заметным встроенным компрессором, который работает только в узкой зоне наилучшего восприятия звука — большую часть времени он прозрачен, но в этой зоне он формирует сигнал ровно настолько, чтобы его можно было услышать.
4. Экспериментальные предсказания
- Слабая анизотропия кадра: скорость сигнала зависит от выравнивания с uᵃ
- Затухающее → распространяющееся преобразование при модуляции смещения QCT
- Управляется Нарушение ограничения Цирельсона
- Масштабирование задержки зависит от смещения перехода, а не от толщины барьера
5. Протоколы испытаний
- Двухлабораторный тест QCT: Модуляция смещения в узле A создает коррелированный отклик в узле B за пределами светового конуса.
- Замена движущихся кадров: Повторяется в относительном движении для проверки предпочтительного выравнивания кадров.
- Эванесцентная инъекция: Волновод ниже отсечки, подключенный к зазору QCT, для обнаружения фазово-модулированного восстановления.
6. Роль QCT
Фемтосекундное туннелирование ККТ и поведение NDR создают ограниченную нелинейность, необходимую для управляемая сверхсветовая когерентность. Причинно-следственная связь поддерживается за счет ограничения отсутствия цикла, обеспечивая глобальный порядок.

В итоге: КФС сохраняет относительность почти везде, допуская при этом структурированный сигнальный конус, активный только в определённых квантовых средах, таких как ККТ. Эта структура вводит проверяемые предсказания для сверхсветовой, но причинно-последовательной коммуникации.
Эта статья является частью серии статей, посвященных необъяснимому явлению, которое я наблюдал в 1986 году в Ирландии:
- НЛО над заливом Голуэй. Глава 1: Встреча в Солтхилле 1986 года
- Отчет о черном НЛО: Принц Чарльз, реактивный самолет и ночь воздушных тайн
- НЛО над заливом Голуэй Глава 2: Экстрасенсорный сигнал бедствия от потерпевшего крушение НЛО
- НЛО над заливом Голуэй Глава 3: Ирландские Туата Де Дананн как космические гости
- НЛО над заливом Голуэй. Глава 4: Обратный инжиниринг квантово-связанного транзистора
- Квантово-связанный транзистор (QCT): Усиление пустоты
- Может ли информация распространяться быстрее света? - Не нарушая физику?

