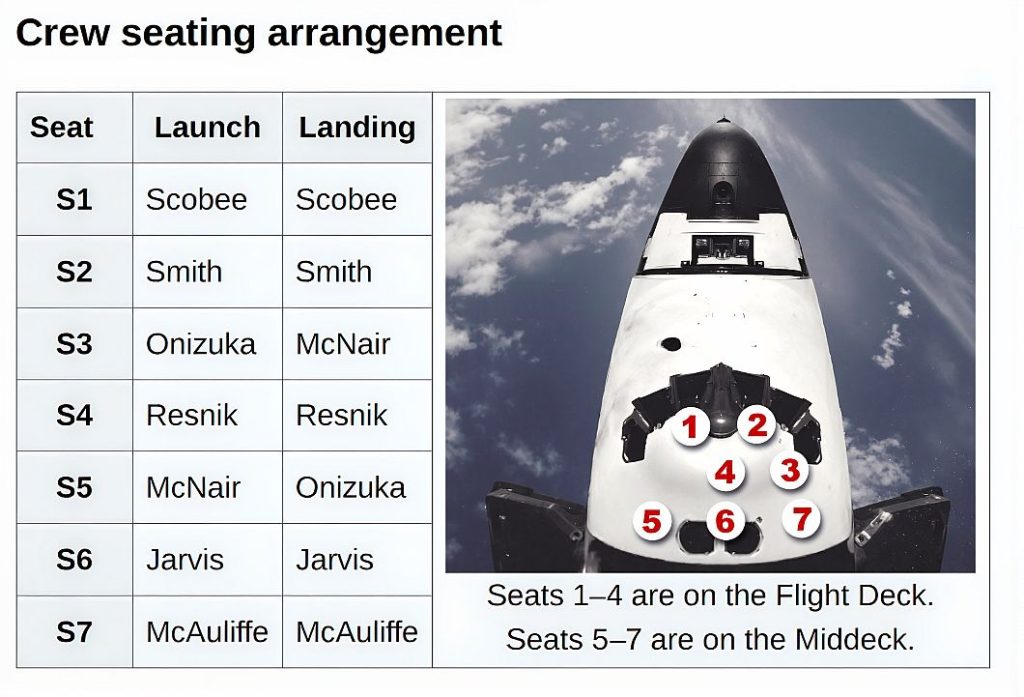
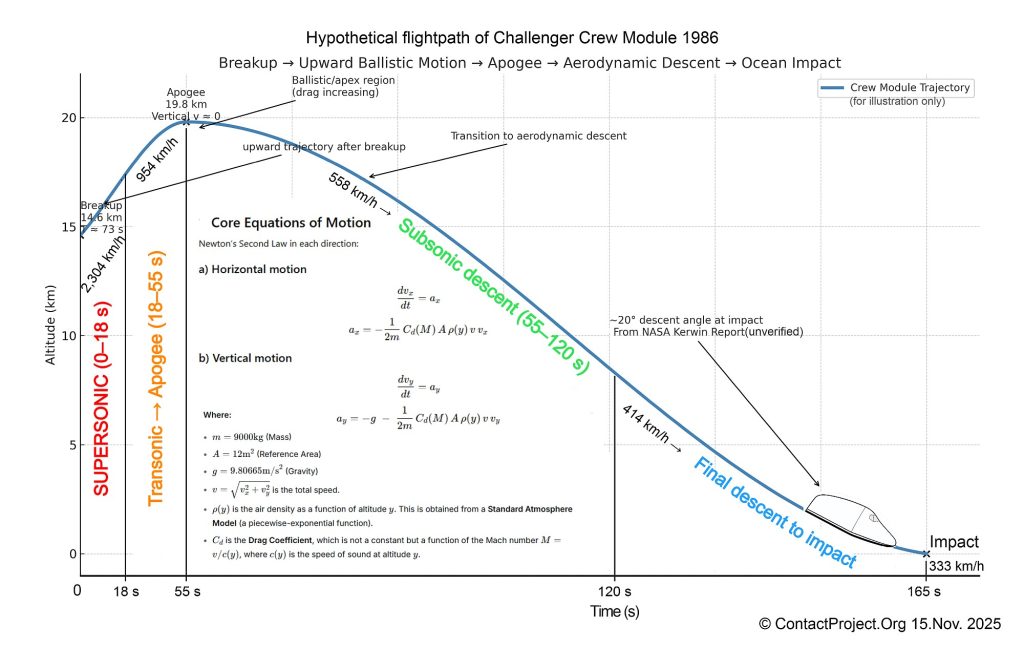
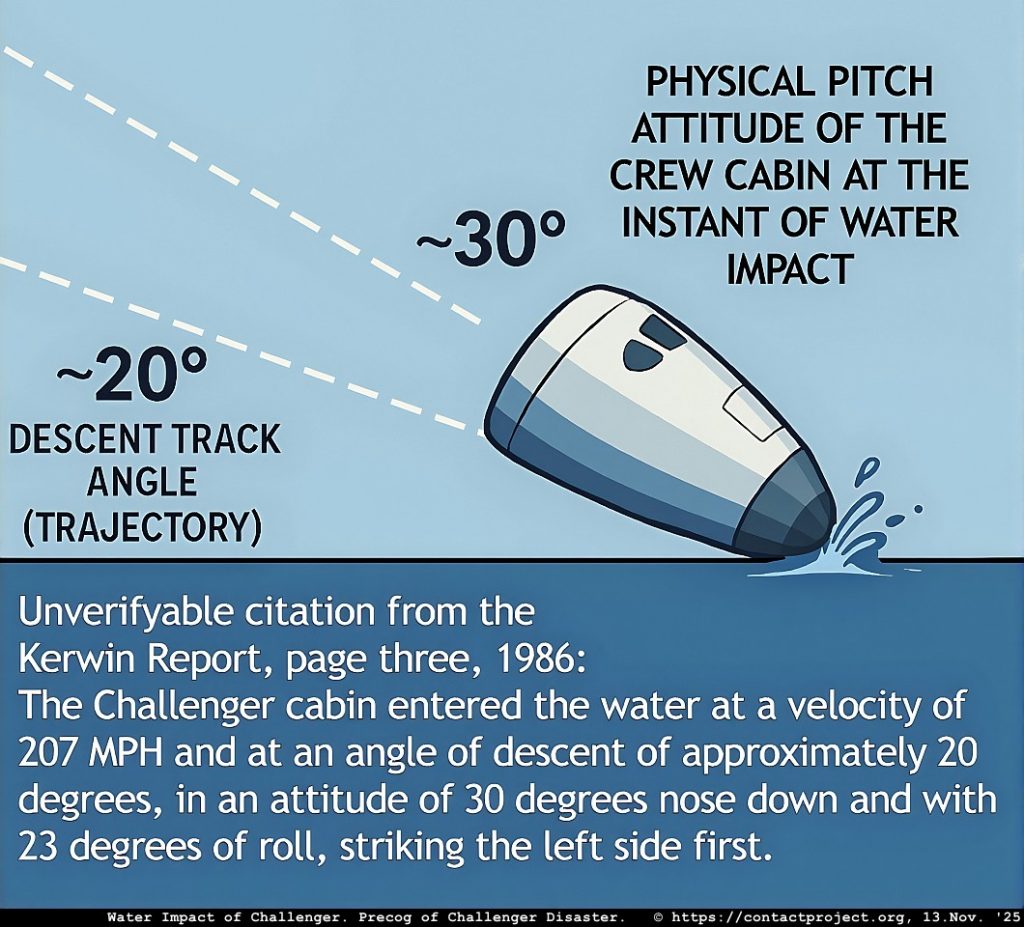
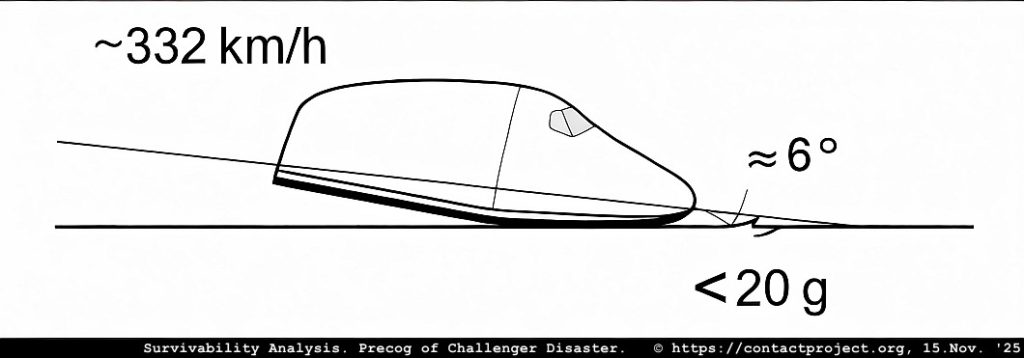
预计阅读时间:32分钟
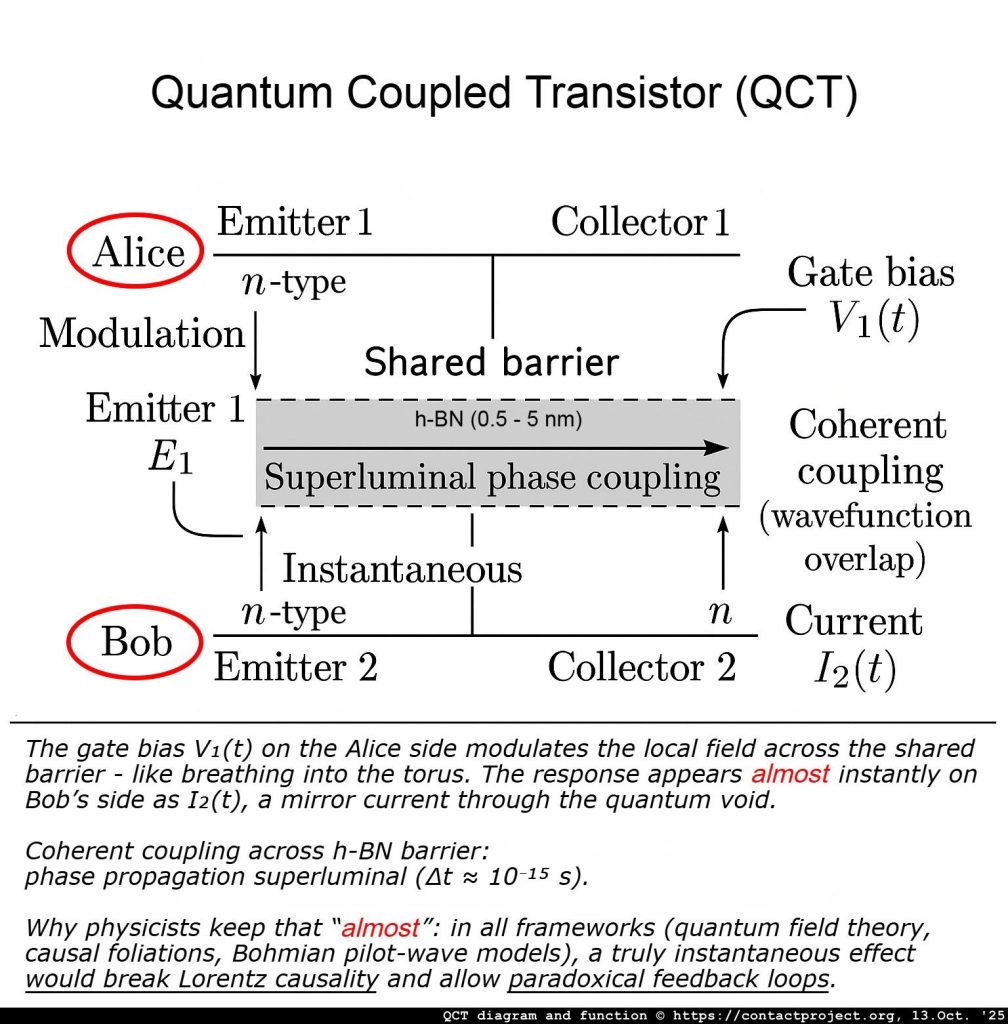
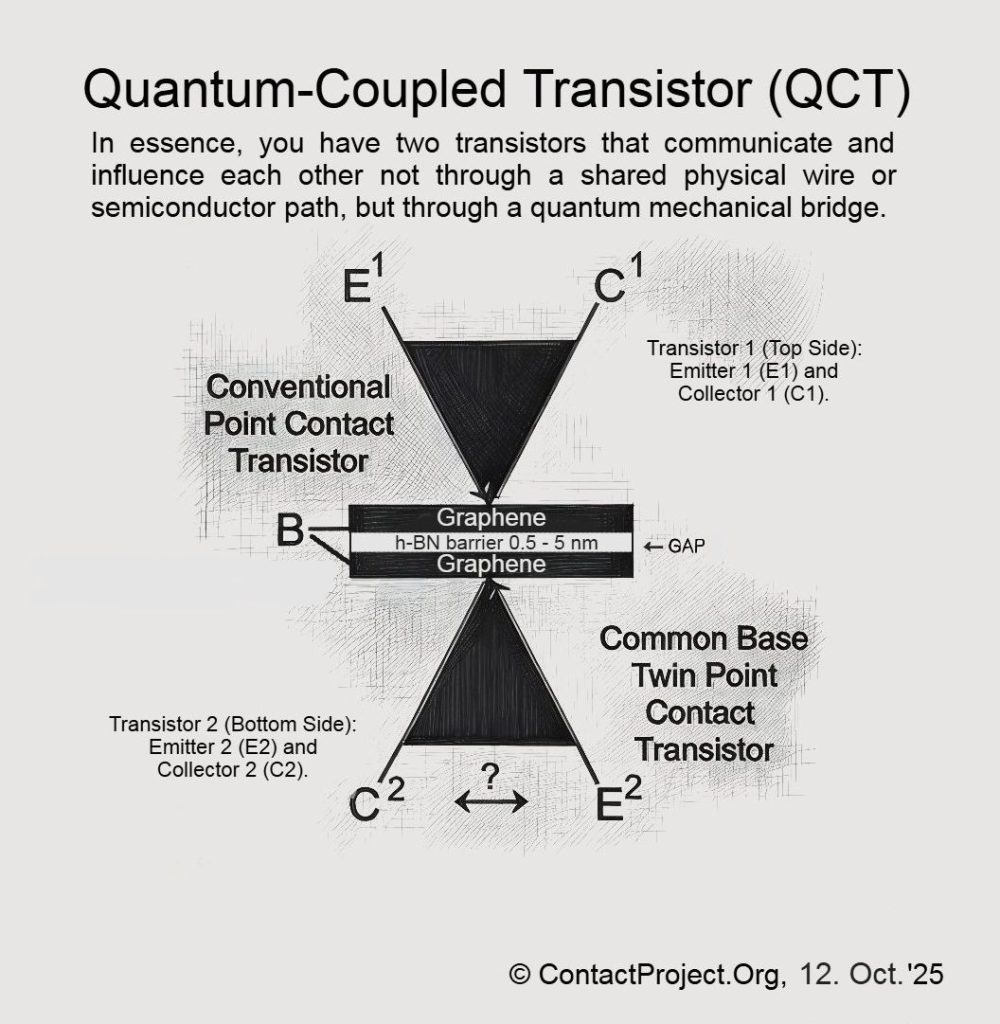
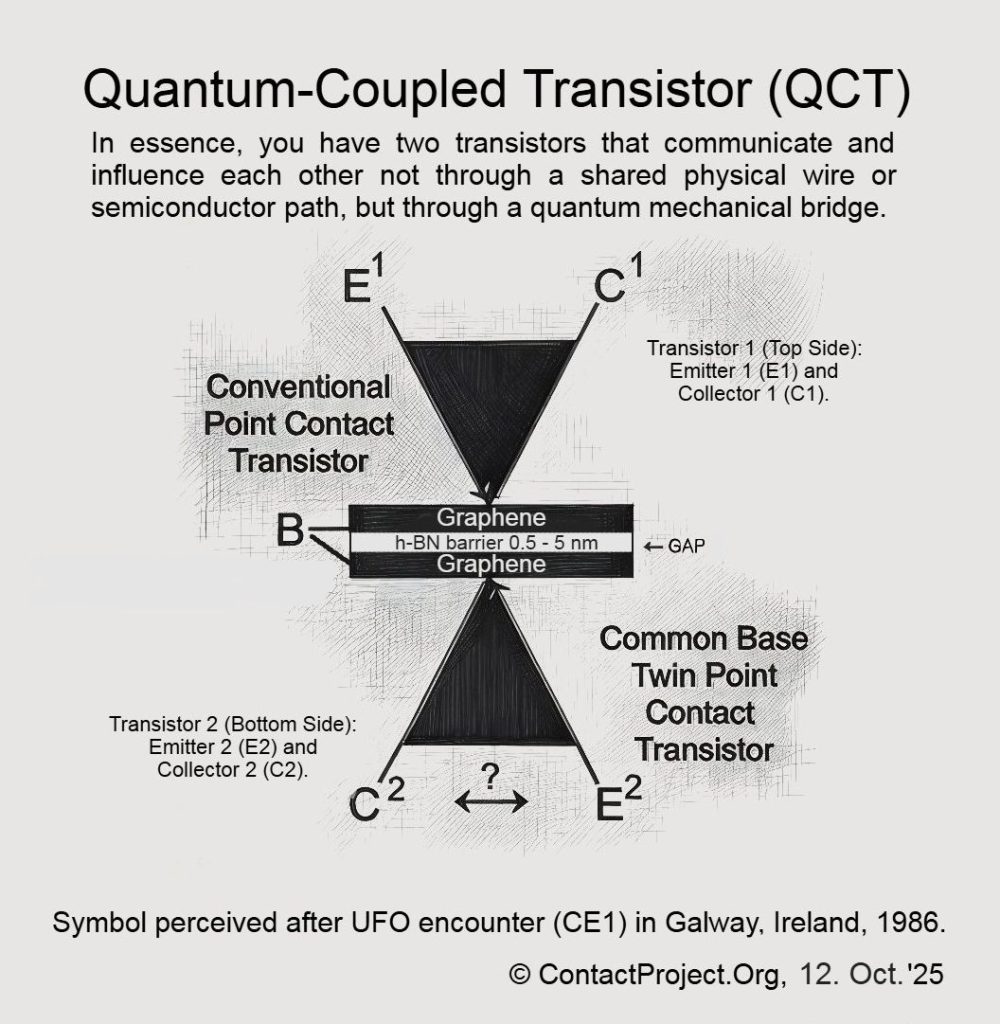
因果叶状信号传导的逻辑 的理论 因果叶状信号(CFS) 提出时间包含隐藏层,使得量子系统之间能够实现有限的超光速相干性。研究人员可能很快就会利用 量子耦合晶体管(QCT) ——双石墨烯纳米器件——直接测试这些效应,并确定它们是否可以在不违反已知物理定律的情况下发生。
从本质上来说,CFS 提出了一个发人深省的问题: 如果某些类型的波(例如倏逝波或近场波)可以比光速更快地共享相位信息,但仍保留因果关系,情况会怎样?
如果真是这样,时空或许并非完全均匀。它可能包含一种微妙的内部结构——时间的“分层”,信息在每一层内略微向前移动,但整体上保持一致。
按照这种观点,宇宙就像一本浩瀚宇宙之书的页面般展开:每一页都按完美的顺序翻动,即使有些页面翻得比其他页面稍快一些。CFS 提供了一种更精妙的相对论视角——它允许结构化的超光速相干性,同时保持因果关系的完整。
第二部分 因果叶状信号 (CFS)
核心公理
运动学和动力学
量子规则与守恒
实验预测
测试协议
QCT 的作用
1. 核心公理
全球时间叶序: 时空拥有一个优先的全局切片(宇宙时间,由类时间矢量定义 你 )。所有信号——光速和超光速——都按照这种叶状结构排序。放大信号锥: 除了光锥之外,还存在针对特定介质或场(χ)的更宽的“信号锥”。时间顺序保护: 可解性约束动态禁止闭合信号回路。运营地点: 标准实验保持洛伦兹不变;偏差仅在启用的介质中发生。
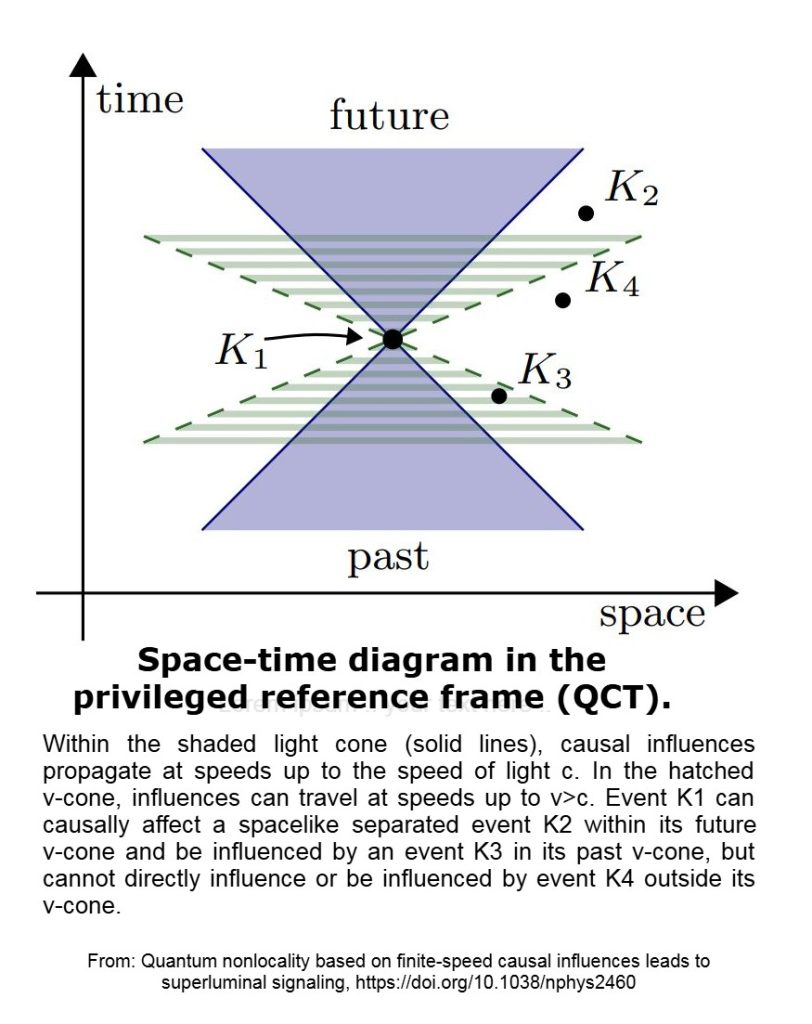
基于有限速度因果影响的量子非局域性导致超光速信号 2.运动学和动力学
首选框架: 与 CMB 静止框架大致对齐。信号场(χ): 与电磁载体弱耦合,扩大因果锥。超光速特性: 偏二氟乙烯 在启用的媒体中展示 g 光锥之外的传播。无循环约束: 积分条件可防止时间减少的因果循环。
3. 量子规则与守恒 我们构建了一个微小的区域(QCT 间隙),在这个区域内,量子近场可以被轻轻地塑造,这样几乎无法探测到的、比光还快的 模式 出现在其他随机数据中——足够小以保证物理安全,足够清晰以在实验室中测试。
如果上面的简洁语句对你来说有意义,那么你可以扩展红线 量子规则 无沟通定理 受控 松弛 该规则 在此处进行探索。
[点击打开] 放松无通信定理: 在启用媒体中,非线性/后选择动态允许微小经典容量> 0。
索赔(操作): 启用介质 (例如,QCT间隙充当χ启用的近场), 弱局部非线性 or 明确的后选择 可以产生一个 小而有限的经典容量 C>0 在不违反整体幺正性或玻恩规则的情况下,类空分离方之间。设置 ρAB 是 Alice 和 Bob 共享的二分状态。在具有局部 CPTP 地图 和 没有 在选择之后,Bob 的简化状态与 Alice 的选择无关:
ρB′=TrA[(ΦA⊗IB)(ρAB)]=ρB, (无信号)
在 启用 QCT 区域,将 Alice 的控制操作建模为 弱非线性 扰动 CPTP地图 :
ΦA(V)(⋅)=ΛA(⋅)+ε\mathcal{N}_A^{(V)}[⋅], 0<ε≪1,[/latex]其中 [latex]V 是爱丽丝的控制(例如,层间偏差), ΛA 是 CPTP 和 \mathcal{N}_A^{(V)} 是有界非线性函数,仅在 χ 启用的介质。
Bob 的状态变为
ρB′(V)=TrA[(ΦA(V)⊗IB)ρAB]=ρB(0)+εΔρB(V),
-
ΔρB(V)=TrA [(NA(V)⊗IB)ρAB].\Delta\rho_B(V)=\mathrm{Tr}_A\!\Big[\big(\mathcal{N}_A^{(V)}\otimes \mathbb{I}_B\big)\rho_{AB}\Big].ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].
If \Delta\rho_B(V_0)\neq \Delta\rho_B(V_1) ,那么 Bob 的结果统计数据(略微)取决于 Alice 的选择 V ,实现经典通信 \伐普西隆 .
对于 POVM \{我的\} 对于 Bob 来说,检测概率是
P(y∣V)=Tr[MyρB′(V)]=P0(y)+εΔP(y∣V),ΔP(y∣V):=Tr[MyΔρB(V)]。
信号弱时容量 让 Alice 发送一个二进制符号 X\in\{0,1\} 通过选择 V\in\{V_0,V_1\}。 . 鲍勃测量 Y\in\{0,1\} 。 定义
\delta := P(Y=1\mid V_1)-P(Y=1\mid V_0)=\varepsilon\,\Delta P + O(\varepsilon^2),
具有基线错误概率 p:=P(Y=1∣V0) .
对于二进制输入、二进制输出通道 小信号限制 ∣\delta|\ll 1 , 香农容量 承认二次近似
C \;\approx\; \frac{\delta^2}{2\ln 2}\,\frac{1}{p(1-p)} \;+\; O(\delta^4), \qquad C>0\ \text{iff}\ \delta\neq 0 .
因此任何非零 \三角洲 (因此任何非零 \伐普西隆 顺序依赖 V ) 得到 有限 C>0 .
后选的作用 如果鲍勃(或联合巧合电路) 后选 在结果窗口上 W 有成功概率 pW , 有条件 状态是
\rho_{B\!\mid W}(V)\;=\;\frac{\Pi_W\,\rho_B'(V)\,\Pi_W}{\mathrm{Tr}\!\big[\Pi_W\,\rho_B'(V)\big]}, \qquad \Pi_W=\Pi_W^\dagger=\Pi_W^2.
由于标准化 \mathrm{Tr}[\Pi_W\rho_B'(V)] ,映射 \rho'_B \mapsto \rho_B^{\mid W} is 非线性的 ,并且条件统计数据可以获得 V -依赖,即使 无条件 无信号平等成立。在实践中,后选择将有用速率缩放为 pW :
C_{\mathrm{eff}} \approx p_W ,C。
一致性条件 为了避免全球性病症:
本土化: \mathcal{N}_A^{(V)} 仅限于 χ 启用区域(例如,QCT间隙)。小: \伐普西隆 足够小以保持稳定性和能量界限。全局幺正性与玻恩规则: 整体动力学保持 CPTP;偏差(如果有的话)仅限于条件局部探测器图(后选择)或介质内的弱非线性部分。
紧凑语句 \boxed{ \begin{aligned} &\Phi_A^{(V)}=\Lambda_A+\varepsilon\,\mathcal{N}_A^{(V)},\quad \varepsilon\ll 1,\\ &\rho_B'(V)=\rho_B^{(0)}+\varepsilon\,\Delta\rho_B(V),\quad \Delta\rho_B(V)=\mathrm{Tr}_A\!\big[(\mathcal{N}_A^{(V)}\!\otimes\!\mathbb{I})\,\rho_{AB}\big],\\ &\exists\,M:\ \delta=\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_1)\big]-\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_0)\big]\neq 0 \\ &\Rightarrow\ C \approx \dfrac{\delta^2}{2\ln 2\, p(1-p)} \;>\;0,\quad C_{\text{eff}}\approx p_W\,C\ \text{(带后选择)}. \end{aligned}}
以下是对这个简洁数学陈述的分解和事实核查: 该数学表达式是量子信息论中一个结果的表示,涉及计算具有微小扰动的量子信道的容量。它将量子信道的物理描述与最终的信道容量联系起来,并结合了状态扰动、输出状态的可区分性以及后选择效应等概念。让我们分解每个部分来验证其组成部分:
通道和状态扰动
\Phi_A(V) = \Lambda_A + \epsilon N_A(V), \epsilon \ll 1 :这描述了一个量子信道 \Phi_A 作用于系统 A。它由一个主要的、恒定的部分组成 \Lambda_A 和一个小扰动 \epsilon N_A(V) ,在 Moku:Pro 上 \epsilon 是一个小参数,V 是信道的一些可控参数。这是表示轻微调制或噪声量子信道的标准方法。 \rho_B'(V) = \rho_B(0) + \epsilon \Delta\rho_B(V) :这显示了通道对较大量子态的一部分的影响。它表明子系统 B 的输出状态, \rho_B'(V) ,是初始状态的稍微扰动版本 \rho_B(0) . 扰动 \Delta\rho_B(V) 与小参数成正比 \epsilon . \Delta\rho_B(V) = Tr_A[(N_A(V) \otimes I)\rho_{AB}] :这是系统 B 状态的一阶扰动的显式形式。它是通过取部分迹(Tr_A )在系统 A 上,通道的扰动部分对更大的纠缠态的作用 \rho_{AB} 这是量子力学规则的标准、正确的应用。
国家的可区分性
\exists M: \delta = \epsilon Tr[M\Delta\rho_B(V_1)] - \epsilon Tr[M\Delta\rho_B(V_0)] \neq 0 :这是建立非零信道容量的关键步骤。它指出存在一个测量算符(厄米算符)M,它可以区分对应于两种不同信道参数设置的扰动状态, V_1 和 V_0 . 数量 \三角洲 表示两个输出状态的测量值 M 的期望值的差异。 \delta \neq 0 是两种状态至少在原则上可以通过实验区分的条件。
信道容量
C \approx \frac{\delta^2}{2\ln{2}p(1-p)} > 0 :这是一个关键结果,可能是 Holevo 容量的近似值,或在小极限下对通道容量的相关度量 \三角洲 容量C是衡量信息能够可靠地通过信道发送的最大速率的指标。术语 \delta^2 是可以预料的,因为对于小扰动,容量通常与输出状态可区分性的平方成比例。 2\ln{2} 是从自然信息单位(NAT)转换为比特的标准。术语 p(1-p) 分母中的表示正在针对特定输入集合评估容量,其中两个状态(对应于 V_0 和 V_1 ) 的概率为 p 和 1-p。当 p=1/2 ,这是一个常见的假设。
后选有效容量
C_{eff} \approx p_W C (含后选择):此部分描述使用后选择时的有效容量。后选择是一种仅考虑部分测量结果的技术,有时可能会放大微弱信号。 p_W 将是成功后选择的概率(“后选择概率”)。有效容量 效率 由于许多初始状态被丢弃,因此概率会降低。这是后选择方案中一个众所周知的权衡:你可能会得到更清晰的信号,但会丢失相当一部分数据,从而降低整体信息传输速率。
人工智能事实核查:结论
QCT:介绍 Alice 和 Bob QCT:介绍 Alice 和 Bob In 标准量子理论 和 信息科学 , 爱丽丝 和 短发 是经典的替身——“每个人”实验者用来说明当双方共享信息时量子系统如何表现。
它们最早出现在 20 世纪 70 年代初:爱丽丝想向鲍勃发送一条消息,而窃听者 Eve ,试图拦截它。这个想法流行起来,物理学家们很快就采用了相同的名称来描述量子实验——尤其是那些涉及 纠葛 , 隐形传送 以及沟通的局限性。
在量子力学中,爱丽丝和鲍勃通常操作两个独立的实验室。他们共享一对纠缠粒子,并独立进行测量。然而,即使结果相互关联,他们也无法用它们发送超光速信息。在标准量子理论中,局部读数总是看起来像白噪声——直到他们后来互相比较,隐藏的模式才显现出来。
我们的转折(仅在启用的介质内): 在一个非常具体的、精心设计的区域——比如 hBN带隙 QCT 的微小、精心限制的非线性效应或“只保留这些事件”的后选择可以将噪声的微观部分变成 非常微弱但真实的信号 。它仍然很小,但不再是白噪声了。
日常类比: 收音机里突然出现一阵静电风暴(随机出现),但如果你稍微调整一下天线,只选择合适的时机,就能听到电台的低语。静电风暴依然存在,但现在它已经形成了规律。
设置(谁做什么) 两党 - 爱丽丝 和 短发 - 共享一个相关的量子装置。通常情况下,Alice 在本地所做的 不 改变鲍勃自己所看到的东西。 QCT 间隙内部 ,爱丽丝的控制(一个微小的、高速的偏置模式)稍微重塑了她这边的局部测量规则,这种方式很重要 内 那个缝隙。这种微小的重塑可能会留下 指纹 关于鲍勃测量的内容——总体上仍然很嘈杂,但现在 统计上推动 由爱丽丝选择。
比喻: 爱丽丝在一块磨砂玻璃(隧道屏障)后面晃动着手电筒。鲍勃看不见手电筒,但他身旁隐约可见的微光却随着爱丽丝的晃动而变化。
爱丽丝和鲍勃用手电筒类比证明了放松无通信定理 鲍勃应该看到什么(确凿的证据) 如果没有发生超出标准量子规则的事情,鲍勃的数据看起来就像随机抛硬币一样——没有任何与爱丽丝的选择相关的模式。 如果启用的媒介确实发挥了作用, 那么 Bob 的噪声数据中隐藏着一个 微小、可重复的相关性 使用 Alice 的模式 - 可以通过交叉检查时间戳来检测,并且关键的是显示 before 任何普通的光速信号都可以到达 (>C) .
比喻: 两个鼓手相距很远;如果鲍勃的麦克风在声音传播之前听到与爱丽丝的节奏一致的微弱节拍,那么他们之间就存在一些不寻常的东西。
“容量”(可容纳多少信息) 想想 通过这种微弱的效果,你每秒可以挤出多少比特。
如果相关性确实 零 ,容量为 零 - 没有消息。
如果相关性是 微小但不为零 ,容量为 微小但不为零 - 你可以发送 一些 信息(缓慢地),这在物理上已经是一件大事了。
比喻: 爱丽丝隔着一堵厚墙敲击着一条信息。每次敲击几乎都无法传递信息,但只要有时间和耐心,信息最终还是会传递给鲍勃。
后期选择(仅保留好的帧) 后选择 意味着你只保留通过过滤器(“窗口”)的测量运行。这可以使隐藏的模式更清晰——但你会丢弃大部分数据,所以你的 有效利率 滴。你获得 明晰 , 失去 吞吐量 。如果目标是证明这种影响存在,那么这是公平交易。
比喻: 观看流星雨但只计算最亮的条纹 - 您可以更清楚地看到图案,但每小时记录的事件较少。
一致性条件(我们如何避免悖论) 为了保持物理学的合理性和因果性,我们施加了三个护栏:
本土化: 任何奇异效应 受限 严格限制在工程区域(QCT间隙)。在区域之外,正常物理规律占主导地位。小: 效果 小 - 足以衡量,但不足以摧毁系统。全球保护: 当你观察时,概率和能量就会平衡 全 实验。局部的怪癖,全球的簿记。
比喻: 安全的测试台:法拉第笼内可能会有火花飞溅,但不会泄漏到房间内。
[点击打开] 全球 天生规则 保存: 局部探测器响应可能会略有偏差。P(i) = |\langle i | \psi \rangle|^2, \quad \sum_i P(i) = 1。 全球保护 和 局部偏差 .
全球保护: 所有叶理切片的总概率保持标准化:\int_{\Sigma_t} \sum_i P(i,t),d^3x = 1, \Sigma_t 由叶状矢量定义 u^a .
局部偏差: 在启用的介质(例如 QCT 隧道间隙)内,局部探测器统计数据可以表现出概率权重的小的非线性偏移,而全局集合平均值仍然遵循 Born 规则。
1.局部非线性响应模型 P_0(i) = \operatorname{Tr}(\rho,\Pi_i), 协调 \ rho 是密度矩阵, \Pi_i = |i\rangle\langle i| 是投影仪。在具有弱非线性耦合的启用介质中 \伐普西隆 ,有效的局部探测器响应为:P_{\text{loc}}(i) = \frac{\operatorname{Tr}(\rho,\Pi_i) + \varepsilon,f_i(\rho,\chi)}{\sum_j [\operatorname{Tr}(\rho,\Pi_j) + \varepsilon,f_j(\rho,\chi)]}, \qquad 0<\varepsilon\ll 1.[/latex]这里 [latex]f_i(\rho,\chi) 是信号场引起的一个小的校正项 \智 或 QCT 的衰减耦合,分母重新正则化总概率以保持 \sum_i P_{\text{loc}}(i) = 1。
2. 示例:双结果测量(二进制检测器) P_0(1) = \operatorname{Tr}(\rho,\Pi_1) = p, \quad P_0(0)=1-p。 具有弱非线性耦合和相位相关校正 f_1 = \alpha,\sin\phi , f_0=-f_1, 局部概率变为P_{\text{loc}}(1) = \frac{p + \varepsilon,\alpha,\sin\phi}{1 + \varepsilon,\alpha,(2p-1)\sin\phi}, \quad P_{\text{loc}}(0)=1-P_{\text{loc}}(1). \伐普西隆 :P_{\text{loc}}(1) \approx p + \varepsilon,\alpha,\sin\phi,[1 - p(2p-1)]. \phi (例如,量子计算机断层扫描中的偏置调制或隧道共振)。经过多次运行或全局积分后,这些偏差会逐渐平均,从而恢复玻恩期望 \langle P_{\text{loc}}(1)\rangle = p.
3. 整体(全局)修复 \langle P(i) \rangle = \int_{\Sigma_t} P_{\text{loc}}(i, x, t),d^3x。 f_i 积分为零,\int_{\Sigma_t} f_i(\rho,\chi),d^3x = 0, \sum_i \langle P(i) \rangle = 1。
4. QCT中的物理意义 \varepsilon f_i(\rho,\chi) 在飞秒级探测器中,可能表现为与偏压相关的噪声或过量计数。然而,全局(在较长的积分过程中),归一化成立——没有能量或概率的产生或损失。因此,玻恩规则在全局范围内仍然成立,而局部探测器可能表现出微小的、可重复的、与相位相关的计数率偏差。
总结方程式: \sum_i P(i)= 1。 P_{\text{loc}}(i) = P_0(i) + \varepsilon,\Delta P(i,\chi), \quad \sum_i \Delta P(i,\chi) = 0。
\langle P_{\text{loc}}(i) \rangle = P_0(i), \quad \sum_i \langle P_{\text{loc}}(i) \rangle = 1。
解读概要: 在启用的量子相干层析成像 (QCT) 区域中,局部探测器可能会出现微小的、与偏差相关的概率偏移,但全局系综平均值会精确地保持总概率,这与玻恩规则一致。这种区别允许出现微弱的、可测试的偏差,这些偏差可以作为非线性或后选择动力学的经验指纹,而不会违反核心量子假设。
玻恩规则——量子力学的核心“概率加为 1”规则 - 仍然在全球范围内有效 . 本地 ,在间隙内,探测器响应可以是 略微倾斜 (这就是重点),但当你正确地平均所有因素时,标准规则仍然完好无损。我们只是在改变,而不是打破。
比喻: 哈哈镜会在角落里扭曲你的倒影——但建筑的结构蓝图并没有改变。
[点击打开] 信号预算 :守恒量 Q_{\text{sig}} 限制通信容量。信号预算 ,表示为 Q_{\text{sig}} 它测量总相干场通量——在不违反全球守恒定律的情况下可以交换的最大“信息电荷”。 j_{\text{sig}}^a 与相位相干场交换(类似于概率或能量流)相关。总守恒量为 Q_{\text{sig}} = \int_{\Sigma_t} j_{\text{sig}}^a,u_a,d^3x, 协调 \Sigma_t 是恒定全局时间的超曲面(叶状切片), u_a 是垂直于该切片的局部单元(定义首选框架的相同叶状矢量场),并且 j_{\text{sig}}^a 遵循连续性方程 \nabla_a j_{\text{sig}}^a = 0。 这意味着 \frac{d Q_{\text{sig}}}{dt} = 0, so Q_{\text{sig}} 在启用区域内的所有局部交互下都是保守的。 Q_{\text{sig}} 量化节点(Alice 和 Bob)之间倏逝耦合场中存储的总相干关联能量或相位容量。它不同于电荷或光子数;而是衡量可用于调制的相互相干性的积分程度。任何通信过程都只能重新分配此量,而不能增加它。 C 通过基于 QCT 的通道实现的效果受信号预算的单调函数所限制: C \le f(Q_{\text{sig}}), 协调 f(\cdot) 取决于器件几何形状、退相干率和热噪声。对于小信号、线性响应区域, f(Q_{\text{sig}}) \approx \frac{1}{2N_0},Q_{\text{sig}}^2, 协调 N_0 是隧道结的有效噪声谱密度,得出 C_{\max} \propto Q_{\text{sig}}^2。 因此,较大的相干通量会产生更高的势能容量,但仅限于退相干破坏相位连续性的程度。考虑两个 QCT 节点(Alice 和 Bob),它们仅通过一个倏逝隧穿场连接。设 \Phi_1(t) 和 \Phi_2(t) 分别为它们的瞬时相势。定义通过耦合间隙的相干信号电流为
j_{\text{sig}}(t) = \kappa,\mathrm{Im}!\big[\Phi_1^*(t),\Phi_2(t)\big],
\kappa 是与势垒隧穿系数成正比的耦合常数。一个相干间隔内的积分信号预算 温度 is
Q_{\text{sig}} = \int_0^{T_c} j_{\text{sig}}(t),dt = \kappa \int_0^{T_c} \mathrm{Im}!\big[\Phi_1^ (t),\Phi_2(t)\big],dt.
I_{\text{sig}}(t) = j_{\text{sig}}(t),A 为通过有效面积的可测量信号电流 A . \text{SNR}(t) = \frac{I_{\text{sig}}^2(t)}{N_0,B}, 协调 B 是带宽。对相干窗口进行积分可得出总容量界限 C \le \frac{1}{2B\ln 2}\int_0^{T_c}\frac{I_{\text{sig}}^2(t)}{N_0},dt = \frac{A^2}{2B\ln 2,N_0}\int_0^{T_c} j_{\text{sig}}^2(t),dt。 Q_{\text{sig}}^2, 给予 C \le k_B,Q_{\text{sig}}^2, 协调 噓 是一个取决于几何形状和温度的经验比例常数。举一个数值例子,假设一个QCT对以势垒耦合的方式运行 \kappa = 10^{-3}, 相干振幅 |\Phi_1| = |\Phi_2| = 1, 和相干时间 T_c = 10^{-12},\text{s}。 Q_{\text{sig}} = \kappa \int_0^{T_c} \sin(\Delta\phi),dt \近似\kappa,T_c,\sin\langle\Delta\phi\rangle。 \langle\Delta\phi\rangle = \pi/4, Q_{\text{sig}} \approx 7.1\times10^{-16},\text{s}。 N_0 = 10^{-20},\text{焦耳/赫兹} 和 B = 10^{12},\text{Hz}, 容量界限变为 C_{\max} \approx \frac{1}{2B\ln 2}\frac{Q_{\text{sig}}^2}{N_0} \approx 3\times10^2,\text{bits/s}。 Q_{\text{sig,tot}} = Q_{\text{sig}}^{(1)} + Q_{\text{sig}}^{(2)}, 但由于干扰,相应的容量呈亚线性增加: C_{\text{tot}} \le f(Q_{\text{sig,tot}}) < f(Q_{\text{sig}}^{(1)}) + f(Q_{\text{sig}}^{(2)})。[/latex]这体现了相干性的有限性:相干性可以共享,但不能自由地放大。总而言之,[latex]Q_{\text{sig}} 是一个守恒标量,表示通过启用介质的总相干场通量。它定义了系统的最大通信预算, C \le f(Q_{\text{sig}}), 确保任何可衡量的容量增加都来自现有 Q_{\text{sig}} 该原理保证了因果关系和热力学一致性,即使对于超光速相位耦合也是如此:信息交换仍然受守恒信号量的限制。
我们对待可用的 相干性 (间隙中近场的有序部分)就像一个 预算 。 您可以 重新分配 它可以发送消息,但你 无法创造更多 从无到有。更多预算→潜在更高的可靠率,直到噪音和热量“停止”。
比喻: 一块用于超薄激光笔的电池:您可以闪烁代码,但闪烁次数受电池限制。
[点击打开] 受限非线性 :通过限制+能量界限避免的病理受限 - 局域于有限的、能量受限的时空区域内,并且仅通过保持全局幺正性的通道与外部环境耦合。量子耦合晶体管 (QCT) 提供了这样一个自然边界。非线性项仅在 启用介质 - 隧穿间隙或 χ 场域 - 其中衰减相耦合和负微分电阻 (NDR) 允许弱自相互作用。在该区域之外,标准线性量子力学完全成立。
形式上,让整个系统演化算子写成 \mathcal{U}(t) = \mathcal{T}\exp!\left[-\frac{i}{\hbar}!\int (H_0 + \varepsilon,H_{\text{NL}}),dt\right], 协调 H_0 是标准的厄米哈密顿量, H_{\text{NL}} 是有界非线性贡献,并且 \varepsilon \ll 1 是一个在 QCT 区域之外消失的激活参数。约束条件为 \operatorname{supp}(H_{\text{NL}}) \subseteq \Omega_{\text{QCT}} ,这意味着非线性相互作用在空间上被限制在启用介质中 \Omega_{\text{QCT}} . 如果交换子 [H_{\text{NL}},H_0] 具有紧支撑和非线性能量密度
\mathcal{E} {\text{NL}} = \langle\psi|H {\text{NL}}|\psi\rangle
满足
\mathcal{E} {\text{NL}} \le \delta E {\text{th}},
协调 \delta E_{\text{th}} 是局部热涨落尺度。这确保了非线性反馈不能自我放大到超出物理噪声极限。
从操作上来说,限制意味着地图 \Phi:\rho\mapsto\rho' 仅在 χ 启用子空间内是弱非线性的
\mathcal{H} {\chi},
而在补集上保持完全正值且迹保持(CPTP)。从数学上讲,
\Phi = \Phi {\text{CPTP}} \oplus (\Phi_{\text{CPTP}} + \varepsilon \mathcal{N}),
- \mathcal{N} 表示受限非线性校正。因为 \varepsilon \rightarrow 0 在QCT边界处,非线性效应不会传播到能隙之外。这可以避免全局不一致性,并强制因果闭合:超光速相位效应可能存在于局部层理结构内,但无法形成闭合信号环路或任意传播。
从热力学角度来看,非线性约束确保了从真空中提取能量是不可能的。激活的NDR区域充当受控反馈元件,可以放大倏逝场,但始终在约束范围内 P_{\text{输出}} \le P_{\text{输入}} + \Delta E_{\text{存储}} 任何瞬态增益都由局部场存储补偿,从而维持整体能量平衡。因此,该系统表现为一个封闭在保守边界内的非线性谐振器。
在因果叶状信号 (CFS) 框架中,这种空间和能量限制保证了稳定性:非线性动力学在不改变全局幺正性的情况下修改局部统计量。量子计算机成为 能量有界非线性岛 嵌入线性量子连续体中。
QCT 的 h-BN 间隙就像一个 法拉第笼用于量子奇异性 ——一个微型沙盒,常规规则可以安全地弯曲而不会被打破。在这个密封区域内,该装置可以放大和回收能量,使其刚好足以揭示微弱的超光速图案,但严格的热量和能量限制使其无法失控。类比:就像建造一个 防火墙放大器 :它可以在虚空中低语,但永远不会违反包含它的物理定律。
[点击打开] Thermo Bounds (增益与噪声温度)热熔胶 表达了这个限制:启用介质中的放大和相干传输必须遵循涨落耗散原理,确保设备的任何配置都不能提取净自由能或违反第二定律。
在平衡状态下,隧道间隙中波动的谱功率密度为 S_V(f) = 4k_B T_{\text{eff}} R_{\text{eq}}(f), 协调 T_{\text{eff}} 是耦合结的有效温度, R_{\text{eq}}(f) 是动态电阻,在NDR偏置下可能变为负值。当QCT提供小信号增益时 G(f) ,涨落耗散定理要求增益和噪声温度的乘积保持有界: G(f)T_{\text{eff}} \ge T_0, 协调 T_0 是环境的物理温度。这确保任何局部放大必然会引入补偿噪声,从而保持熵平衡为非负值。
这种约束的量子类似物源于场算符的对易关系。对于任何作用于玻色子模式的放大器 \hat a_{\mathrm{in}} 和 \hat a_{\mathrm{出}} ,必须保持正则交换,即[,\hat a_{\mathrm{out}},,\hat a_{\mathrm{out}}^{\dagger},]=1. \hat a_{\mathrm{out}}=\sqrt{G},\hat a_{\mathrm{in}}+\sqrt{G-1},\hat b_{\mathrm{in}}^{\dagger},\qquad [,\hat b_{\mathrm{in}},\hat b_{\mathrm{in}}^{\dagger},]=1,
在QCT中,该噪声对应于由倏逝场的热涨落和量子涨落引起的隧道电流的随机分量。有效增益-噪声权衡可以写成 G_{\text{QCT}} = 1 + \frac{P_{\text{out}} - P_{\text{in}}}{k_B T_{\text{eff}} B}, 服从 P_{\text{出}} \le P_{\text{入}} + k_B T_{\text{效果}} B, 协调 B 是带宽。该不等式表达了相干放大的热力学上限。
实际上,随着h-BN势垒上的偏压增加,NDR区域能够将能量重新注入衰减模式,从而有效地放大近场。然而,这种增益具有自限性:一旦局部噪声温度升至 T_{\text{eff}} = T_0 + \Delta T_{\text{NDR}}, 系统达到热稳定状态。进一步增加偏置会以热量的形式耗散额外的能量,而不是增加相干性。因此,热噪声基底就像一个天然的“刹车”,稳定系统,防止失控放大。
因此,热边界可以概括为连接信息增益、能量输入和熵产生的守恒定律: \Delta I \le \frac{\Delta E}{k_B T_{\text{eff}} \ln 2}。 这种不等式定义了任何基于 QCT 的通信通道或因果信号实验的最终效率:单位能量消耗可实现的信息率不能超过保持一致性的熵成本。
从更广泛的角度来看,Thermo Bound 是信号预算约束的热对应物。 Q_{\text{sig}} 限制总相干通量, T_{\text{eff}} 限制了该通量内的可用放大倍数。它们共同将QCT的操作窗口定义为一个量子谐振但热力学封闭的系统。除了允许与环境交换的能量之外,不会产生或损失任何能量,并且总熵变保持非负: \frac{dS_{\text{tot}}}{dt} = \frac{P_{\text{in}} - P_{\text{out}}}{T_0} \ge 0。
本质上,Thermo Bound 确保 QCT 发挥 热力学兼容量子放大器 - 能够在其启用区域内实现相位相干增益和超光速耦合,但始终受到保持全局因果关系和物理定律的底层能量熵平衡的约束。
如果你试图放大间隙中的近场,你也会提高它的 有效噪声温度 。这其中存在一个权衡:增益越高,噪音也就越大。大自然会强制这种平衡,所以你 不能 获得免费能源或无限、清晰的放大。
比喻: 调高吉他音箱的音量:信号更响,但嘶嘶声也更多。有时,额外的音量只会增加噪音和热量。
[点击打开] 最小模型:启用介质中的非线性检测器/放大器动力学 在量子计算机隧道势垒等启用区域,我们假设测量或放大图中存在弱的、状态相关的非线性。该图表示为 N_{\chi} ,对局部密度矩阵进行运算 \ rho 与信号场耦合的子系统 \智 它保留了总概率(迹保留),但引入了受控非线性,足以产生有限但微小的经典容量。
1。 定义 N_{\chi}(\rho) = \frac{A_{\chi} \rho A_{\chi}^{\dagger}}{\mathrm{Tr}(A_{\chi} \rho A_{\chi}^{\dagger})}, A_{\chi} = I + \epsilon, F(\rho, \chi) 是一个弱依赖于信号场的非线性算子 \智 以及当前系统状态 \ rho . 小参数 \epsilon \ll 1 控制非线性程度。
分母的标准化强制 \mathrm{Tr}[N_{\chi}(\rho)] = 1 ,确保地图保留痕迹且物理一致。
2. 线性限制 在规划婴儿食品行业的工艺要求时,安全性和可靠性是工艺设计中最重要的方面。 ε = 0 ,该模型简化为标准量子测量: N_{\chi}(\rho) \to \rho' = \frac{M \rho M^{\dagger}}{\mathrm{Tr}(M \rho M^{\dagger})}, M 是测量运算符(POVM元素)。
3. 有效动力 对于弱非线性,该映射导出一个有效的演化方程:
\dot{\rho} = -\frac{i}{\hbar}[H, \rho] + \epsilon, \mathcal{L} {\chi}[\rho],
协调
\mathcal{L} {\chi}[\rho]
表示将系统状态与信号场耦合的非线性函数。 \mathcal{L}_{\chi}[\rho] = f(\chi),(\rho^2 - \rho,\mathrm{Tr}[\rho^2]), \rho^2 = \rho ).
4.信息容量 关键结果是后选或非线性检测可以产生小而有限的经典容量 C_{\mathrm{eff}} 穿过原本只有纠缠(无信号)的通道: C_{\mathrm{eff}} \approx p_{W}, C, p_{W} 是非线性后选择窗口的成功概率,并且 C 是理想化信令信道的容量。
这对应于启用媒体中严格的无通信行为的微小但可衡量的偏差:
C_{\mathrm{eff}} > 0, \qquad C_{\mathrm{eff}} \ll C_{\mathrm{经典}}。
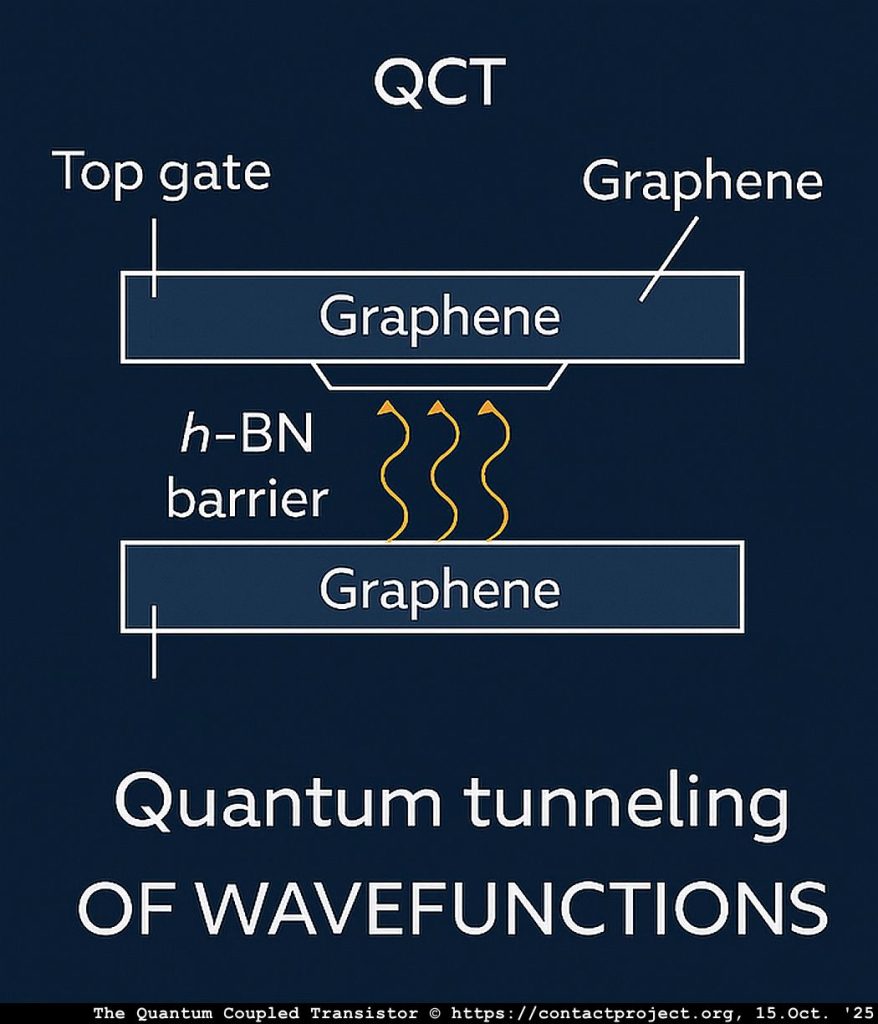
5. 物理示例:QCT势垒耦合 在量子耦合晶体管中,两个石墨烯层充当通过量子屏障连接的局部相干探测器。\chi(t) 表示跨 h-BN 隧道区域的衰减相势。 T_{\chi}(V) = T_{0} \exp[-\alpha (1 - \beta V + \epsilon, \Phi_{\chi}(\rho))], \Phi_{\chi}(\rho) 是将局部波函数相干性与场态耦合的弱反馈项。
6. 保护与稳定 为了防止失控放大,非线性项满足守恒约束: \mathrm{Tr}[\rho,\mathcal{L}_{\chi}[\rho]] = 0, \epsilon .
7。 解释 结果是 最小修改的量子规则 :
我们 不会 重写量子力学。我们正在添加一个 微小的、依赖于状态的扭曲 间隙内的探测器/放大器如何响应——刚好足以让微弱的图案叠加在噪声上。间隙外,一切都正常且线性。间隙内,响应是 略 上下文感知(这是“非线性”部分),我们保留它 界 所以没有什么可以逃避。
比喻: 带有精巧内置压缩器的麦克风仅在微小的最佳位置起作用 - 大多数时候它是透明的,但在该位置它会将信号塑造成足以被听到的形状。
4.实验预测 5. 测试协议
双实验室 QCT 测试: 节点 A 处的偏置调制会在光锥之外的节点 B 处产生相关响应。移动帧交换: 重复相对运动以测试首选帧对齐。瞬时注射: 截止以下波导耦合到 QCT 间隙以检测相位调制恢复。
6. QCT的作用 QCT 的飞秒隧穿和 NDR 行为产生了一个受限的非线性,这是 可控的超光速相干性。 通过无循环约束来维持因果关系,确保全局秩序。
总结: CFS 几乎在任何地方都保持相对论,同时允许结构化信号锥仅在特定量子介质(例如 QCT)中激活。该框架引入了 可检验的预测 用于超光速但因果一致的通信。
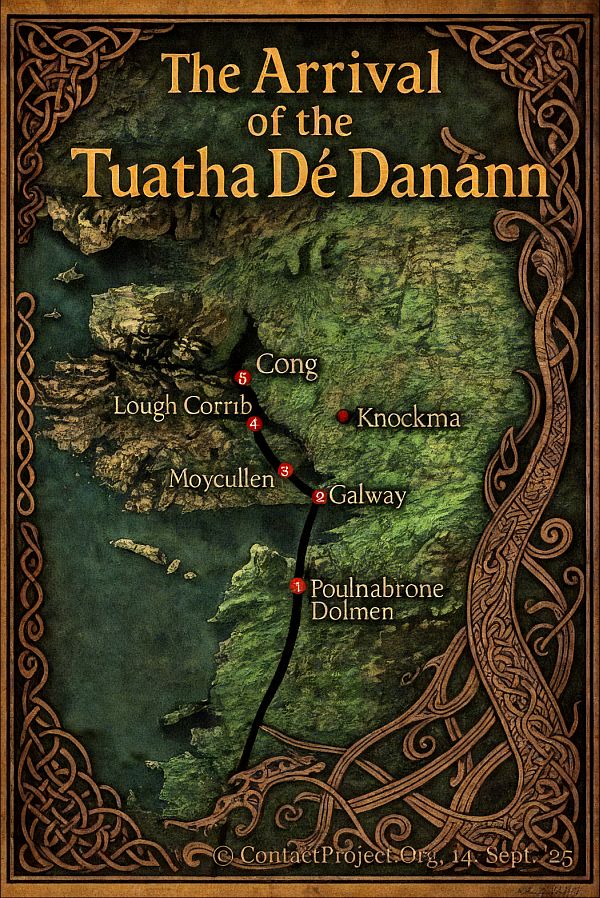
本文是系列文章的一部分,全部与我 1986 年在爱尔兰看到的一次不明原因的目击事件有关:
对挑战者号航天飞机灾难的预知 戈尔韦湾上空的不明飞行物 第 1 章: 1986年萨尔特希尔遭遇战 黑色UFO报告 :查尔斯王子、巨型喷气式飞机和空中神秘之夜戈尔韦湾上空的不明飞行物 第二章: 来自坠毁UFO的心灵求救信号 戈尔韦湾上空的不明飞行物 第二章: 爱尔兰人 Tuatha Dé Danann 饰演 宇宙访客 了解 听:“Tuatha Dé Danann 的到来” 音乐视频 戈尔韦湾上空的不明飞行物 第 4 章: 量子耦合晶体管的逆向工程 量子耦合晶体管(QCT): 放大虚空 信息传播速度能比光快吗 - 不破坏物理学?